Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Alaor Chaves- Ed: 1º - Capítulo 23.Exercícios e Problemas - Ex. 16

Calcule a indutância mútua entre o fio (longo) vertical e a espira quadrada mostrados na Figura 23.19.

Passo 1

Fala pessoal, tudo tranquilo?

Nesse problema queremos calcular a indutância mútua entre o fio e a espira quadrada de lado a mostrada na figura. Para isso, vamos achar o fluxo do campo magnético produzido pelo fio sobre a espira.

O primeiro passo é definir um sistema de coordenadas:

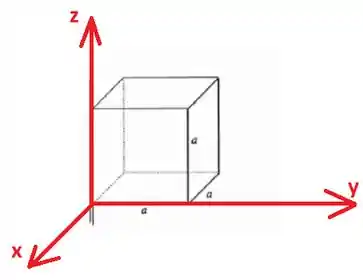
Com essa definição de sistema de coordenadas temos que a espira se localiza no plano y = a com - a ≤ x ≤ 0 e 0 ≤ z ≤ a . O versor normal à espira é

n ^ = - y ^

O campo magnético produzido pelo fio infinito é

B → = μ 0 I 2 π r φ ^ ,

onde r = x 2 + y 2 e φ ^ = - s e n   φ   x ^ + cos ⁡ φ   y ^ são das coordenadas cilíndricas.

Para achar o fluxo, fazemos

Φ B = ∬ B → ⋅ n ^   d A = ∬ μ 0 I 2 π r - s e n   φ   x ^ + cos ⁡ φ   y ^ ⋅ - y ^   d A = - μ 0 I 2 π ∬ cos ⁡ φ r   d A

Passo 2

O elemento de área d A pode ser escrito como

d A = d x   d z

Assim,

Φ B = - μ 0 I 2 π ∫ 0 a d z   ∫ - a 0 cos ⁡ φ r   d x

A integral em z é imediata:

Φ B = - μ 0 a I 2 π   ∫ - a 0 cos ⁡ φ r   d x

Para fazer a integral em x lembramos que

cos ⁡ φ = x r → cos ⁡ φ r = x r 2

Por outro lado

r 2 = x 2 + y 2

Nesse caso temos y = a , de modo que

r 2 = x 2 + a 2

Com isso, temos que

Φ B = - μ 0 a I 2 π ∫ - a 0 x x 2 + a 2   d x

Para fazer essa integral fazemos a mudança de variável

u = x 2 + a 2 → d u = 2 x   d x → x   d x = d u 2

Com isso,

Φ B = - μ 0 a I 2 π ⋅ 1 2 ∫ 2 a 2 a 2 1 u d u = μ 0 a I 4 π ∫ a 2 2 a 2 1 u d u

Na última passagem eu inverti o sinal com os limites de integração. Fazendo essa integral encontramos

Φ B = μ 0 a I 4 π ln ⁡ 2

Passo 3

A indutância mútua é dada simplesmente pela razão do fluxo pela corrente:

L = Φ B I

Com isso,

L = μ 0 a 4 π ln ⁡ 2

Problema resolvido 😉.

Resposta

L = μ 0 a 4 π ln ⁡ 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em New Hampshire. o valor médio do componente horizontal do campo magnético da Terra, em 1912, era de 16 μ T e a inclinação média era de 73°. Qual era o correspondente módulo do campo magnético da Ter
A Terra tem um momento de dipolo magnético de 8.0 x 1^22 J/T. ( a) Que corrente deveria ser estabelecida numa única espira, rodeando a Terra em seu equador magnético, para produzir este momento de dip
Uma superfície gaussiana tem a forma de um cilindro circular reto, de raio igual a 12,0cm e comprimento de 80,0cm. Através de uma de suas extremidades, penetra um fluxo magnético de 25,0 μ Wb. Na outr
O campo magnético da Terra pode ser aproximado como o campo de um dipolo magnético, com componentes horizontal e vertical, num ponto distante r do centro da Terra. dados por B h = μ 0 μ 4 π r 3 cos ⁡
Use os resultados apresentados no Problema 13 para calcular o módulo e o ângulo de inclinação do campo magnético da Terra no polo norte geográfico. (Sugestão: O ângulo entre o eixo magnético e o eixo