Enunciado
Química - Young and Freedman - Vol 4- Ed: 12º - Capítulo 43.Exercícios - Ex. 10
Calcule a perda de massa, a energia de ligação (em ) e a energia de ligação por núcleon de:
- Um núcleo de nitrogênio ;
- De um núcleo de hélio .
- Como se comparam os resultados dos itens (a) e (b)?
Passo 1
Olá, tudo bem? Vou ajudar você nessa questão! Vamos lá?
Primeiro vou relembrar você qual fórmula calcula todas essas quantidades que o problema nos pede. É a equação do teu livro texto:
Aqui temos que é a energia de ligação do núcleo, é a massa do átomo neutro que contém o núcleo e é a energia de ligação por núcleon. A expressão entre parênteses indica a perda de massa. E para termos as energias de ligação em devemos usar o fato de que . O valor de é e de é . O número de nêutrons é encontrado fazendo .
E vou colar aqui a tabela que tem os valores das massas atômicas dos átomos neutros de alguns nuclídeos:
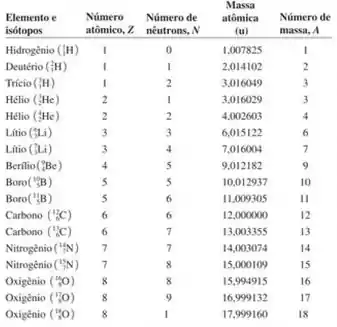
Beleza? Agora vamos aplicar esses conceitos nos núcleos que foram dados =)
Passo 2
Letra a)
Aqui temos e . Consultando a tabela do passo anterior temos que a massa atômica do é . Juntando tudo isso na fórmula da energia de ligação teremos:
A perda de massa é de , e agora substituindo por teremos a energia de ligação :
Então a energia de ligação desse núcleo é . E dividindo esse valor por teremos a energia de ligação por núcleon:
Certinho até aqui? Beleza!
Agora para fazer a letra (b), é só proceder da mesma forma, apenas modificando as massas e o número atômico =)
Passo 3
Letra b)
Aqui temos e . Consultando a tabela do passo anterior temos que a massa atômica do é . Juntando tudo isso na fórmula da energia de ligação teremos:
A perda de massa é de , e agora substituindo por teremos a energia de ligação :
Então a energia de ligação desse núcleo é . E dividindo esse valor por teremos a energia de ligação por núcleon:
Passo 4
Letra c)
A energia de ligação por núcleon do é ligeiramente menor do que a energia de ligação por núcleon encontrada para o .