Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 26.Exercício - Ex. 12
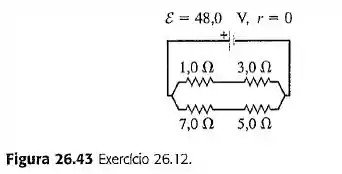
Calcule a resistência equivalente do circuito indicado na Figura 26.43 e determine a corrente que passa em cada resistor. A bateria possui resistência interna desprezível.
Passo 1
Substitua as combinações de séries de resistores por seus equivalentes. Na rede paralela resultante, a voltagem da bateria é a voltagem em cada resistor.
O circuito é esboçado na figura a seguir:
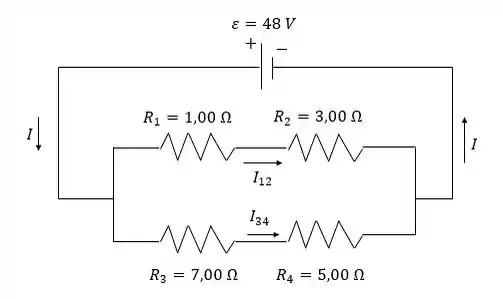
Passo 2
e em série têm um equivalente resistência de:
e em série têm uma resistência equivalente a:
Passo 3
O circuito é equivalente ao circuito esboçado na Figura a seguir:
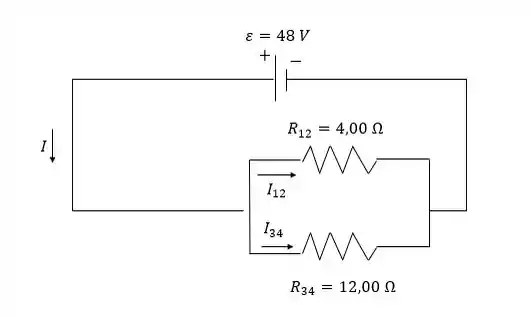
e em paralelos são equivalentes a , e nos dá que:
Isso implica que:
Assim,
Passo 4
A tensão através de cada ramo da combinação paralela é , então:
Como , então:
Resposta
A corrente é de aos resistores de e , e de aos resistores de e .
Exercícios de Livros Relacionados
Dois resistores, R 1 e R 2 , podem ser ligados em paralelo ou em série entre os terminais de uma fonte ideal de força eletromotriz ε Estamos interessados em que a potência dissipada pela combinação do
Uma lâmpada de120V com dois filamentos pode operar em três níveis de potência: 100 ,200 e300W . Um dos filamentos queima. Depois disso, a lâmpada funciona com a mesma luminosidade (dissipa a mesma pot
Na Fig. 27-82, uma fonte ideal de força eletromotriz ε =12,0V é ligada a um circuito cujasresistências s ã oR 1=6,00Ω ,R 2=12,00Ω ,R 3=4,00Ω ,R 4=3,00ΩeR 5=5,00Ω ã . Qual é a diferença de potencial da
No circuito da figura, R 1 = 20Ω e R 2 = 60Ω . Para que valor de R a potência dissipada em R é afetada o mínimo possível por pequenas variações de R?
Um fio uniforme de resistencia R é cortado em três partes iguais. Uma das partes forma um circulo e é conectada entre as outras duas partes (Figura 26.37). Qual é a resistencia entre as extremidades o