Enunciado
Física - Moysés - Vol. 3- Ed: 1º - Capítulo 10.Problemas - Ex. 1
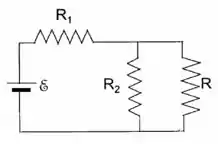
No circuito da figura, e . Para que valor de R a potência dissipada em R é afetada o mínimo possível por pequenas variações de R?
Passo 1
Vamos lá!
Pela configuração podemos ver que está em paralelo com . Então podemos dizer que
Considerando que pelos resistores , e passam as correntes , e , respectivamente podemos escrever que
Passo 2
Outra coisa que podemos dizer é que
Sabendo que a corrente passa pelo resistor 1 e depois se divide, temos
Passo 3
Substituindo (3) em 2, temos
Lembrando que a potência é
Podemos escrever para o resistor R que a potência dissipada é
Passo 4
Para verificar o mínimo de variação da potência em R, temos
Resposta
Exercícios de Livros Relacionados
Um cabo de 20,0 m de comprimento consiste de um núcleo cilíndrico em níquel maciço, com 10,0 cm de diâmetro, envolto por uma casca cilíndrica em cobre, com 10,0 cm de diâmetro interno de 20,0 cm de di
71- Um resistor R 1 consome uma energia elétrica P 1 , quando conectada a uma f e mϵ . Quando o resistor R 2 é conectado a mesma f e m , ela consome energia elétrica P 2 . Em termos de P 1 e P 2 , qua
A Figura 26.75 mostra uma convenção geralmente usada nos diagramas de circuitos. A bateria (ou outra fonte de tensão) não é mostrada explicitamente. Fica implícito que o ponto no topo do diagrama, ind
Um certo galvanômetro possui resistência de 65Ω e indica uma deflexão até o fundo da escala quando passa uma corrente de 1,50m A em sua bobina. Ele deve ser substituído por um segundo galvanômetro, qu
A ponte de Wheatstone. O circuito indicado na Figura 26.80 denomina-se ponte de Wheatstone e é usado para determinar uma resistência desconhecida X por comparação com três resistores M , N e P , cujas