1. Calcule a velocidade de um feixe de elétrons que sofre, simultaneamente, a ação de um campo elétrico de e de um campo magnético igual a , com ambos os campos ortogonais ao feixe e perpendiculares entre si e sabendo que o feixe não sofre nenhum desvio.
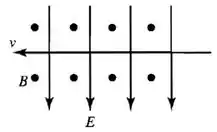
2. Faça um diagrama para mostrar as orientações relativas dos vetores , e .
3. Quando o campo elétrico é removido, qual é o raio da órbita do elétron? Qual é o período dessa órbita?

letra b)

A velocidade precisa ser perpendicular ao campo magnético e ao campo elétrico, para a força magnética poder se anular com a força elétrica e a partícula não sofrer nenhum desvio.

Podemos então fazer da seguinte forma:

letra c)

Quando o campo elétrico é removido, a partícula irá descrever uma trajetória circular.

Então:

Como o campo e velocidade são perpendiculares :

Isolando o raio:

Agora precisamos calcular o período dessa órbita. Podemos usar a relação: