Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 29.3 - Ex. 41
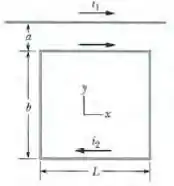
Na figura 29-66, um fio retílíneo longo conduz uma corrente e uma espira retangular conduz uma corrente . Suponha que , e . Em termos dos vetores unitários, qual é a força a que está submetida a espira?
Passo 1
Nesse problema temos um fio retílíneo longo que conduz uma corrente e uma espira retangular conduz uma corrente . temos que supor que , e e nosso objetivo, em termos dos vetores unitários, é descobrir qual é a força a que está submetida a espira.
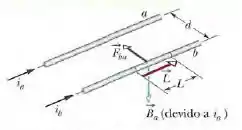
A força entre duas correntes paralelas na presença do campo magnético externo é dada por:
em que é o vetor comprimento do fio. Podemos ver na figura acima, os vetores e são mutuamente perpendiculares e, portanto, de acordo com a equação para fios retilíneos longos, podemos escrever:
Onde é a permissividade magnética do vácuo, é o comprimento do fio, e as correntes e a distância entre os fios.
Veja só! 👀
Passo 2
Nesse exercício, podemos calcular os módulos das forças exercidas sobre os lados da espira paralelos ao fio longo usando a expressão mostrada acima. No entanto, as forças exercidassobre os lados perpendiculares teriam que ser calculadas através de integrais do tipo:
Entretanto, por conta da simetria do problema, as forças exercidas sobre os lados perpendiculares ao fio longo se cancelam.
Tranquilo até aqui? 🤔
Passo 3
Para os lados paralelos, temos:
Substituindo pelos valores dados no enunciado, temos
E aponta na direção do fio. Assim, na notação de vetores unitário:
E aí! o que achou? Responde Aí! 😉
Resposta
A força é: