Um caminhão carregado, com massa total de 3 toneladas, viajando para o norte a 60 km/h, colide com um carro de massa total 1 tonelada, trafegando a leste a 90 km/h, num cruzamento. Calcule em que direção e de que distância o carro é arrastado pelo caminhão, sabendo que o coeficiente de atrito cinético no local do acidente é 0,5.

Faaala galerinha, como essa colisão entre veículos é tipicamente inelástica vamos escrever

Isolando a velocidade final temos

Agora bora olhar pro nosso esquema galera

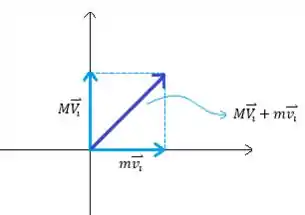
Como as direções são norte e leste podemos valcular o módulo do vetor apenas por Pitágoras, fica assim

Logo, pra calcular o módulo da velocidade final basta dividirmos por . Fica assim ó

Galera, vamos escrever a força que a tua no caminhão e carro após a colisão

Como a força de atrito é a força resultante fazemos

Por torricelli

Aqui temos

Substituindo temos