Enunciado
Física - Curso de Física Básica - Mecânica Volume 1 - 5ª Edição - Herch Moysés Nussenzveig- Ed: 5º - Capítulo 9.Problemas - Ex. 18
O espalhamento elástico de um próton por um núcleo alvo desconhecido em repouso é observado numa câmara de bolhas, onde existe um campo magnético perpendicular ao plano de movimento do próton. Verifica-se que o próton é desviado de e que o raio da curvatura da sua trajetória é reduzido por um fator de 0,946 em consequência da colisão. Identifique o núcleo alvo.
Passo 1
Galera, vamos começar pela informação de que o raio da trajetória é reduzido por um fator de 0,946. Observando para a lei de força magnética temos o seguinte
Sabendo que a a força magnética forma um ângulo de com o vetor velocidade a trajetória é circular e a força magnética é a resultante centrípeta, logo
Já que temos
Uma vez que o campo magnético e a carga do próton são constantes, o módulo do momento linear do próton cai pelo mesmo fator de 0,946. Show!
Passo 2
Vamos agora olhar para nossa colisão
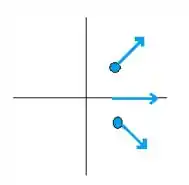
Considerarando agora os vetores momento linear das partículas
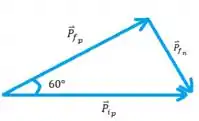
Aqui é o vetor momento final do próton que foi defletido em , é o vetor momento inicial do próton e é o vetor momento final do núcleo desconhecido.
Pela lei dos cosenos temos
Vamos usar a relação que encontramos no passo anterior que nos diz que
Fica assim
Precisamos de outra equação pra completar a solução galera, pra isso temos que buscar outra informação no enunciado. Isso mesmo que você pensou! A colisão é elástica e a energia cinética se conserva.
Vamos agora juntar nossas equações e para deixar tudo em função do momento linear inicial do próton . Vem comigo!
Eliminando os termos em comum dos dois lados fica assim
A ideia é descobrir a razão entre as massas pra identificar o núcleo pelo seu peso, então
Matamos! Nosso núcleo desconhecido tem massa atômica 9, pois sua massa é 9 vezes maior que a de um próton. Portanto, estamos falando de um isótopo de berílio com 4 prótons e 5 neutrôns, ou seja .