Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 5.Problemas - Ex. 91
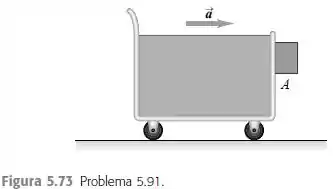
Qual deve ser a aceleração do carrinho da Figura para que o bloco A não caia? O coeficiente de atrito estático entre o bloco e o carrinho é . Como seria o comportamento do bloco descrito por um observador no carrinho?
Passo 1
Eaee, belezinha?? Bom... o enunciado nos dá o seguinte sistema que representa um carrinho que está com uma aceleração e que tem um bloco:
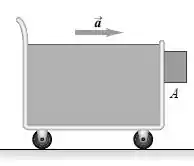
Queremos encontrar a aceleração do carrinho para que o bloco A não caia.
O coeficiente de atrito estático entre o bloco e o carrinho é .
Também queremos saber como seria o comportamento do bloco descrito por um observador no carrinho.
Para resolver isso, temos que analisar as forças que compõem o sistema e aplicar a Segunda Lei de Newton:
Onde é a força resultante, é a massa e é a aceleração.
Passo 2
Bom... O carrinho e o bloco possuem a mesma aceleração, então a força de atrito entre o bloco e o carrinho deve ser suficiente para manter ele em equilíbrio.
Então a força de atrito estático deve ser máxima e igual ao peso do objeto.
Onde é a aceleração da gravidade.
Passo 3
Agora na horizontal temos que a força normal , pela segunda lei, deve ser igual ao produto da massa pela aceleração do sistema :
E sabemos que a força de atrito, por definição, se relaciona com a força normal:
Passo 4
Agora é só igualar as duas formas de escrever a força de atrito:
Cortamos as massas e temos finalmente a aceleração:
Quanto menor o coeficiente de atrito , maior deve ser a aceleração do carrinho para que o bloco não caia sob a ação da gravidade.
Quem está no carrinho não entende muito bem o que está acontecendo, pois ele se move em um referencial não inercial e para ele e.