Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Curso de Física Básica - Mecânica Volume 1 - 5ª Edição - Herch Moysés Nussenzveig- Ed: 5º - Capítulo 13.Problemas - Ex. 5

Um caminhão transporta um caixote de 200   k g a 90   k m / h numa estrada horizontal. Avistando um obstáculo, o motorista fria, com desaceleração uniforme de 2,5   m / s 2 , até parar. O caixote, em consequência da freiada, desliza pela traseira do caminhão com coeficiente de atrito 0,25 . (a) Qual é a velocidade do caixote no instante em que o caminhão para? (b) A que distância de sua posição inicial na traseira do caminhão o caixote se encontrará, quando para de deslizar?

Passo 1

No referencial do caminhão, vamos trocar a desaceleração pra esquerda por uma aceleração para direita. Vem comigo!

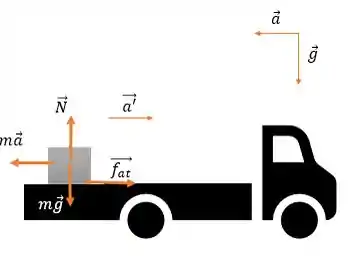
Escrevendo as equações de Newton, temos:

N - P = 0 m a - f a t = m a '

Como N = m g e f a t = μ N :

m a - μ m g = m a '

Logo,

a ' = a - μ g

Substituindo os valores:

a ' = 2,5   m / s 2 - 0,25 ⋅ ( 9,81   m / s 2 )

Assim,

a ' = 0,0475 m s 2     ( i )

Passo 2

Agora vamos achar o instante em que o caminhão para.

v c = v 0 - a t

Convertendo a velocidade para m / s , temos:

v =   90 k m / h × 1   m / s 3,6   k m / h   = 25   m / s

Logo,

0 = 25 m s - 2,5 m s 2 t → t = 10 s

Agora é só usar a aceleração do bloco.

v b = v 0 + a ' t

Então,

v b = 0,0475 m s 2 ⋅ 10   s = 0,475   m / s

Para a distância percorrida:

v b 2 = v 0 2 + 2 a ' Δ x

Substituindo os valores,

0,475 m s 2 = 2 ⋅ 0,0475 m s 2 ⋅ Δ x

Então,

Δ x = 2 , 3 75   m

Resposta

  1. v b = 0,475   m / s
  2. Δ x = 2 , 3 75   m
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Blocos feitos do mesmo material, mas de diferentes tamanhos, são transportados por um caminhão que está se movendo ao longo de uma estrada horizontal reta. Todos os blocos deslizarão se a aceleração d
Um bloco de massa m repousa sobre um plano inclinado em um ângulo de θ com a horizontal. Segue-se que o coeficiente de atrito estática entre o bloco e o plano é(a) μ e ≥ g (b) μ e = t a n θ (c) μ e ≤
Um bloco de massam repousa sobre um plano inclinado em um ângulo de 30 ° com a horizontal, como mostra a figura abaixo. Quais das seguintes alternativas sobre a magnitude da força de atrito estático f
Em um dia de inverno gelado, o coeficiente de atrito entre os pneus de um carro e uma estrada é reduzido para um quarto de seu valor em um dia seco. Como resultado, a velocidade máxima v m á xs e c o
Projetando sua nova casa na Califórnia (nos Estados Unidos, em região geologicamente instável), você a prepara para suportar uma aceleração horizontal máxima de 0,50 g . Qual é o menor coeficiente de