Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 5.1 - Ex. 120
Projetando sua nova casa na Califórnia (nos Estados Unidos, em região geologicamente instável), você a prepara para suportar uma aceleração horizontal máxima de . Qual é o menor coeficiente de atrito estático entre o piso e seu vaso toscano de estimação capaz de evitar que, nessas condições, o vaso deslize sobre o piso?
Passo 1
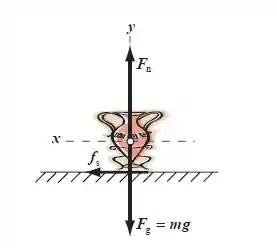
As forças que atuam no vaso são a força gravitacional exercido pela Terra, a força normal exercido pelo chão, e a força de atrito estático , também exercida pelo chão. Podemos aplicar a Segunda Lei de Newton para encontrar o mínimo coeficiente de atrito estático que irá impedir que o vaso escorregue. Olhe o diagrama de forças abaixo:
Passo 2
Aplicando a Segunda lei de Newton no vaso no eixo x:
E no eixo y, como o vaso não sobe e nem desce nesse eixo:
Pela definição de força de atrito estático, temos:
Passo 3
Agora, substituindo essa última equação na primeira do passo 2, temos:
Como