Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 22.Problemas - Ex. 65
Campo elétrico no interior de um átomo de hidrogênio. Um átomo de hidrogênio é constituído por um próton com carga e um elétron com carga . Podemos considerar o próton uma carga puntiforme situada em , o centro do átomo. O movimento do elétron faz com que sua carga seja ‘espalhada’ ao longo de uma distribuição esférica em torno do próton, de modo que o elétron seja equivalente a uma carga por unidade de volume dada por
Em que é o chamado raio de Bohr. Calcule a carga total do átomo de hidrogênio contida em uma esfera de raio centralizada sobre o próton. Mostre que, quando , a carga contida nesse volume tende a zero. Explique esse resultado. Encontre o módulo, a direção e o sentido do campo elétrico produzido pelo átomo de hidrogênio em função da distância . Faça um gráfico do módulo do campo elétrico em função de .
Passo 1
Para iniciarmos esse exercício, precisamos lembrar que a carga elétrica pode ser definida em função da densidade volumétrica de carga e do volume da superfície em questão, ou seja:
Assim, a carga total do átomo de hidrogênio será a soma da carga do próton e da carga do elétron, tal que:
Como o volume do elétron é esférico, ele pode ser escrito como:
Então, a carga total é:
Como o raio do átomo vai de (centro) a (superfície), podemos substituir a variável de integração de para fazendo:
Passo 2
A integral pode ser resolvida através da integração por partes, com e , tal que e :
E, usando a integração por partes novamente com e , tal que e , então:
Portanto:
Substituindo o intervalo de integração:
Passo 3
Logo, a carga elétrica será dada por:
Portanto:
Podemos concluir que, ao olhar essa equação, quando o valor da função exponencial tende a zero e, então, a carga total também tende a zero. Isso ocorre porque o volume total se aproximará de infinito, fazendo com que a carga total do próton e do elétron esteja distribuída em uma pequena parcela do volume de raio infinito e tenha pouca influência sobre o volume.
Passo 4
Visto que a carga total em função do raio da esfera é positivo, então pela lei de Gauss:
Logo:
O campo elétrico é positivo e, por isso, tem fluxo para fora do centro da esfera.
Passo 5
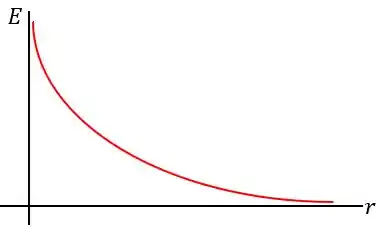
O gráfico do campo elétrico em função do raio é dado por:
