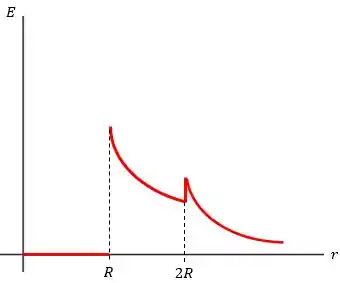
Uma esfera condutora sólida de raio com carga está no interior de uma casca esférica muito fina isolante e concêntrica, com raio e que possui também uma carga . A carga está distribuída uniformemente sobre a casca esférica isolante. Determine o módulo, a direção e o sentido do campo elétrico em cada uma das regiões , e . Faça um gráfico do módulo do campo elétrico em função da distância .

Para saber o campo elétrico em cada situação, precisamos considerar uma superfície gaussiana adequada para cada uma delas.

Primeiramente, supondo uma superfície gaussiana esférica de raio , temos que o seu campo elétrico será é nulo por ser um condutor sólido carregado e não possuir carga em seu interior.

Já a superfície gaussiana de raio envolve a carga da esfera condutora com valor . Logo, o seu campo elétrico será dado pela lei de Gauss:

Tal que isolando o campo elétrico:

Apontando para fora (carga positiva).

Tomando a superfície de raio , ambas as cargas da esfera e da casca estão envolvidas por ela e, logo, possui o dobro do valor do campo elétrico:

E também aponta para fora (carga positiva).