Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Alaor Chaves- Ed: 1º - Capítulo 22.Exercícios e Problemas - Ex. 5

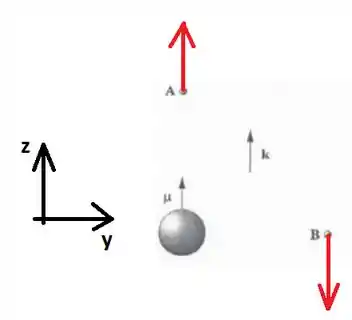
Calcule o campo magnético nos pontos A e B, vistos na Figura 22.14, ambos à distância de 1,0 ⋅ 10 5   k m do centro da Terra.

Passo 1

Eai pessoal, beleza?

A primeira coisa que devemos fazer num exercício assim é definir um sistema de coordenadas:

Eu coloquei o eixo z na direção do dipolo magnético μ → e o eixo y na direção horizontal para ser consistente com o adotado no livro na figura 22.6. Vamos considerar que o dipolo magnético está na origem do sistema de coordenadas, de modo que

B = 0 ,   D ,   0                     A = 0 ,   0 ,   D ,

onde D = 1,0 ⋅ 10 5   k m = 10 8   m . Além disso, o momento de dipolo da terra é dado por

μ = 8 ⋅ 10 22   J / T

Na equação 22.21 do livro foram apresentadas as componentes do campo magnético produzido por um dipolo magnético:

B x = μ 0 μ 4 π ⋅ 3 x z r 5 ,             B y = - μ 0 μ 4 π ⋅ 3 y z r 5               e             B z = μ 0 μ 4 π 3 z 2 r 5 - 1 r 3

Note também que

μ 0 μ 4 π = 4 π ⋅ 10 - 7 ⋅ 8 ⋅ 10 22 4 π = 8 ⋅ 10 15   T   m 3

Eu escrevi esse termo separado pois ele aparece nas três componentes!

Passo 2

No ponto (a), temos

x A = 0 ,                 y A = 0 ,                   z A = D

Assim, temos r = x 2 + y 2 + z 2 = D :

B x = B y = 0                   e             B z = μ 0 μ 4 π 3 D 2 D 5 - 1 D 3 = μ 0 μ 4 π ⋅ 2 D 3

Agora é só fazer continha:

B z = 8 ⋅ 10 15 ⋅ 2 10 8 3 = 16 ⋅ 10 - 9   T

Desta forma, no ponto A o campo é dado por

B → A = 1,6 ⋅ 10 - 8   T   z ^

Passo 3

Já para o ponto B, temos

x B = 0 ,             y B = D ,             z B = 0       →         r = D

Assim,

B x = B y = 0                 e             B z = μ 0 μ 4 π ⋅ 0 - 1 D 3 = - μ 0 μ 4 π ⋅ 1 D 3

Logo,

B z = - 8 ⋅ 10 15 ⋅ 1 10 8 3 = - 8 ⋅ 10 - 9   T

Com isso,

B → B = - 8 ⋅ 10 - 9   T   z ^

A seguir representamos os dois vetores:

Resposta

B → A = 1,6 ⋅ 10 - 8   T   z ^

B → B = - 8 ⋅ 10 - 9   T   z ^

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em uma certa região existe uma densidade de corrente uniforme de 15 A/m^2 no sentido positivo do eixo z. Considere a curva fechada formada pelos três segmentos de rela que ligam os pontos dc coordenad
Duas espiras quadradas, condutoras, transportam correntes de 5.0 A e 3.0 A como é mostrado na Fig. 31-53. Qual é o valor de B ds para cada uma das curvas fechadas mostradas?
A densidade de corrente no interior de um fio cilíndrico comprido e maciço, de raio a está na direção do eixo central e varia linearmente com a distância radial r de acordo com J = Jar/a. Determine o
Mostre que um campo magnético uniforme B não pode cair abruptamente a zero quando o percorremos perpendicularmente, como é sugerido pela seta horizontal que passa pelo ponto d na Fig. 31-54. (Sugestão
Um tubo comprido e circular, com um raio externo R transporta uma corrente (uniformemente distribuída), para dentro da página, como é mostrado na Fig. 31-57. Um fio está disposto paralelamente ao tubo