Enunciado
Física - Alaor Chaves- Ed: 1º - Capítulo 18.Exercícios e Problemas - Ex. 10
Um capacitor é feito com uma folha de PVDF (constante dielétrica 11 e rigidez dielétrica ). A folha tem espessura de , e em uma de duas faces é depositado um filme de alumínio com espessura de . A folha é enrolada em torno de uma haste cilíndrica metálica de raio diminuto, formando um cilindro com raio de e altura de . A capacitância do capacitor equivale à da folha de PVDF com filmes de alumínio nas duas faces, cuja largura é e cujo comprimento é proporcional ao número de voltas do rolo. Calcule a capacitância do capacitor.
Passo 1
Fala galerinha, beleza?
Essa questão é bem confusa, bem confusa mesmo! Vou destacar o ponto do enunciado que vamos nos concentrar:
“A capacitância do capacitor equivale à da folha de PVDF com filmes de alumínio nas duas faces, cuja largura é e cujo comprimento é proporcional ao número de voltas do rolo.”
Podemos pensar nesse capacitor como se fossem dois capacitores de placas paralelas em série:
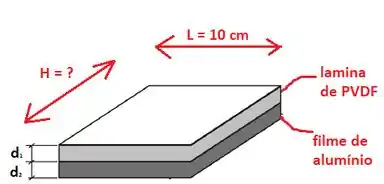
Sabemos que para capacitores em série vale
Para o capacitor com PVDF, temos
Já para o filme de alumínio:
Portanto,
Ou ainda,
Vamos calcular o denominador primeiro:
Sabemos que e . Além disso, e (pesquisei na internet a constante dielétrica do alumínio). Com isso temos
Já sabemos também que , . Então só falta achar para calcular a capacitância usando
Passo 2
O grande segredo do exercício é achar esse , que como foi dito no enunciado, deve ser proporcional ao número de voltas no rolo.
Vamos considerar a seguinte situação: pegue uma folha e vai girando-a em torno de um lápis. Cada volta terá um comprimento , onde vai variando conforme damos várias voltas, já que camadas da folha vão se acumulando. O comprimento total da folha será a soma de cada um desses comprimentos . É isso que temos que fazer nesse problema!
Vamos considerar que a espessura da folha é e vamos dar voltas. O raio da primeira volta é . Já para segunda será , para a terceira e assim por diante...
Note que os raios obedecem a uma progressão aritmética com primeiro termo nulo e razão . Assim, a soma dos primeiros termos dessa PA deve ser dada por
Por outro lado, usando a fórmula do termo geral:
Assim,
Agora vamos relacionar , e por
Desta forma,
A soma de todos os comprimentos é
Com isso podemos calcular a capacitância:
Fazendo as continhas achamos