Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Alaor Chaves- Ed: 1º - Capítulo 26.Exercícios e Problemas - Ex. 5

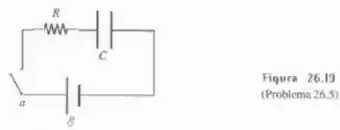
O capacitor da Figura 26.19 está inicialmente descarregado, e a chave é então ligada, fechando o circuito. Mostre que somente metade da energia fornecida pela bateria será armazenada pelo capacitor.

Passo 1

Fala galerinha, beleza?

Esse é um exercício bem legal sobre conservação de energia. Nosso objetivo vai ser calcular a energia dissipada no resistor e ver que ela é exatamente metade da energia fornecida pela bateria. Isso vai indicar que apenas metade da energia fornecida será armazenada no capacitor...

Para isso, consideremos a discussão da seção 26.1.3 do livro, em que se encontra como a carga q do capacitor varia com o tempo no processo de carga:

q t = C E 1 - e - t τ C ,

onde τ C = R C . Para achar a corrente, derivamos a carga com relação ao tempo:

I t = d q d t = C E τ C e - t τ C

Com isso, podemos escrever a expressão para a potência dissipada no resistor e a potência fornecida pela bateria:

P r e s t = R I 2 = R C 2 E 2 τ C 2 e - 2 t τ C = C E 2 ⋅ 1 τ C e - 2 t τ C

P b a t t = E I = C E 2 ⋅ 1 τ C e - t τ C

Repare que as expressões são praticamente iguais, mas o fator 2 na exponencial vai fazer toda a diferença!

Passo 2

Para calcular a energia total dissipada no resistor, integramos a potência no tempo de t = 0 até t = ∞ :

E r e s = ∫ 0 ∞ P r e s t   d t = C E 2 ∫ 0 ∞ 1 τ C e - 2 t τ C   d t

Fazendo a integral, obtemos

E r e s = C E 2 - 1 τ C ⋅ τ C 2 e - 2 t τ C 0 ∞

Para t = ∞ a exponencial se anula e para t = 0 ela dá um, de modo que

E r e s = C E 2 2

Agora fazemos o mesmo com a bateria:

E b a t = ∫ 0 ∞ P b a t t   d t = C E 2 ∫ 0 ∞ 1 τ C e - t τ C   d t = C E 2 - 1 τ C ⋅ τ C 1 e - t τ C 0 ∞

Repare que onde aparecia o fator 2 para o resistor aparece um fator 1 para a bateria! Com isso, temos que

E b a t = C E 2 = 2 E r e s

Logo,

E r e s = E b a t 2

Como E r e s + E c a p = E b a t , segue que

E c a p = E b a t 2

Era isso que o exercício pediu para você mostrar!

Resposta

Demonstração.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

(a) Na Fig. 27-4a, mostre que a potência dissipada em Ré máxima para R = r. (b) Mostre que a potência máxima é P = ε 2 4 r .
O motor de arranque de um automóvel está girando muito devagar e o mecânico não sabe se o problema está no motor, no cabo ou na bateria. De acordo com o manual, a resistência interna da bateria de 12
Na Fig. 27-48, R 1 = R 2 = 10,0 Ω e a força eletromotriz da fonte ideal é ε = 12,0 V . (a) Determine o valor de R 3 que maximiza a potência fornecida pela fonte; (b) determine o valor da potência máxi
Na Fig. 27-83 ,ε 1 =6,00V ,ε 2 =12,0V ,R 1=200ΩeR 2=100Ω . Determine (a) o valor absoluto e (b) o sentido (para cima ou para baixo) da corrente na resistência 1 , (c) o valor absoluto e (d) o sentido
Na Fig. 27-81, as forças eletromotrizes das fontes ideais são ε 1 =20,0V ,ε 2 =10,0V ,ε 3 =5,00V e ε 4=5,00V , e todas as resistências são de 2,00Ω . Determine (a) o valor absoluto e (b) o sentido (pa