Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 24.Problemas - Ex. 72
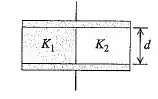
Um capacitor com placas paralelas possui o espaço entre as placas preenchido com duas camadas de dielétricos, uma com uma constante dielétrica e a outra com a constante (veja a figura abaixo). Cada camada possui espessura igual à distância entre as placas e cada camada preenche o espaço entre as placas. Mostre que a capacitância é dada por
Passo 1
De modo geral, podemos escrever a capacitância como sendo:
Como esse capacitor tem dois dielétricos diferentes, podemos dizer que cada região tem uma capacitância diferente, sendo a capacitância equivalente:
Precisamos agora achar as capacitâncias e
Passo 2
Como vimos:
QUando tem um dielétrico:
Mas nesse caso, a área entre as placas está dividida por causa dos dielétricos então a área será .
e o outro:
Passo 3
A capacitância será:
Sendo essa expressão que deveríamos mostrar.
Resposta
Ei, a resposta está no passo a passo :)