78- Um indicador de nível de combustível usa um capacitor para determinar a altura atingida pelo combustível em um tanque. A constante dielétrica efetiva varia de um valor igual a quando o tanque está vazio até um valor , a constante dielétrica do combustível, quando o tanque está cheio. Um circuito eletrônico apropriado pode determinar a constante dielétrica efetiva da camada de ar combinada a camada do combustível entre as placas do capacitor.
Cada uma das suas placas retangulares possui largura e um comprimento (Figura ). A altura do combustível entre as placas é . Despreze qualquer efeito de borda.
Deduza a expressão para em função de .
Qual é a constante dielétrica efetiva quando o tanque está cheio até de seu volume, de volume e até de volume, se o combustível for gasolina ?
Repita a parte para o metanol
Para qual dos dois fluidos esse indicador do nível de combustível é mais prático?
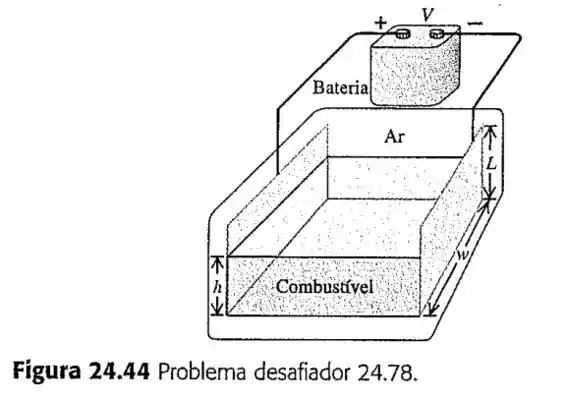
Passo 1
O capacitor de combustível e o capacitor de ar estão em paralelo no tanque:
E as capacitâncias podemos ser escritas como:
Onda quando inteiramente por ar e a área é a área da superfície lateral do tanque, pois os terminais das baterias estão ligadas nelas nos dando algo mais ou menos assim.
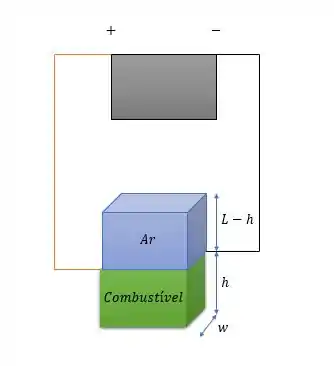
Então a soma das duas capacitâncias (por que estão em paralelo) será:
Isolando os termos temos em comum:
Poém para termos um valor equivalente de devemos ter:
Onde o termo é a área máxima que um dos materiais terá enquanto o termo faz essa regulagem de área para cada uma delas separadamente.
Então devemos isolar desse termo , ou seja
Isso nos dá um valor igual a:
Pois esse valor é a consante do capacitor equivalente entre o ar e o combustível nesse tanque.
Passo 2
Quando a 1 quarto do volume nós temos: e
Pois todas a base estará preenchida.
Então:
Para (volume na metade) nós teremos:
E para (volume em ) teremos:
Passo 3
Agora para temos:
Passo 4
Quanto maior o range (intervalo do menor valor para o maior valor possível) do sensor mais preciso ele será, pois ele terá mais valores intermediários para atuar. Então nesse caso o metano é um melhor combustível para esse sensor.