Enunciado
Física - Halliday - Vol 3- Ed: 4º - Capítulo 27.Questionário - Ex. 2
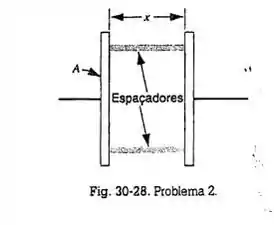
Um capacitor está sendo projetado para operar, com capacitância constante, em um ambiente de temperatura variável. Conforme apresentado na Fig. 30-28, o capacitor é do tipo placas paralelas, alinhadas com o emprego de "espaçadores" plásticos. (a) Mostre que a taxa de variação da capacitância com a temperatura é dada por
onde é a área da placa e é o afastamento entre as placas. (b) Se as placas são de alumínio, qual deveria ser o coeficiente de dilatação térmica dos espaçadores para que a capacitância não varie com a temperatura? (Despreze o efeito dos espaçadores na capacitância.)
Passo 1
Vamos lá resolver mais uma questão juntos?!
Passo 2
E foi isso, viu como foi tranquilo? Vamos pra próxima 😊
Resposta
b.
Exercícios de Livros Relacionados
2 . Cada placa de um capacitor com placas paralelas possui área igual a 9,82c m 2 e a distância entre as placas é de 3,28m m . A carga acumulada em cada placa possui módulo igual a 4,35⋅10 - 8C . As p
1 . Cada placa de um capacitor com placas paralelas possui carga acumulada de módulo igual a 80,0n C e a distância entre as placas é de 2,50m m . As placas estão no vácuo. O campo elétrico entre as pl
12 . Um capacitor cilíndrico possui um condutor interno com raio de 2,2m m e um condutor externo com raio de 3,5m m . Os dois condutores estão separados pelo vácuo e o comprimento total do capacitor é
7 . Um capacitor com placas paralelas e preenchido com ar deve armazenar uma carga de módulo igual a 240,0p C em cada placa quando a diferença de potencial entre as placas é de 42,0V . ( a ) Se a área
11 . Um capacitor esférico contém carga de 3,30n C , quando está conectado a uma diferença de potencial de 220V . Supondo que as placas estejam separadas por vácuo e o raio interno da casca externa se