Enunciado
Física - Halliday - Vol 3- Ed: 4º - Capítulo 27.Questionário - Ex. 8
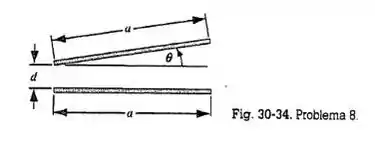
Um capacitor tem placas quadradas, cada uma com lado , fazendo um ângulo com a outra, conforme indicado na Fig. 30-34. Mostre que para um ângulo pequeno, a capacitância é dada por
(Sugestão: O capacitor pode ser dividido em duas tiras diferenciais que estão efetivamente em paralelo.)
Passo 1
Divida a faixa de largura a em N segmentos, cada um com largura Δx=a/N. A capacitância de cada faixa é . Se θ é pequeno então
Como as capacitâncias paralelas se somam,
Resposta
Exercícios de Livros Relacionados
A Figura 17.11 mostra um corte em um capacitor cilíndrico carregado com carga Q . Os raios dos cilindros interno e externa são a e b , respectivamente. O cilindro interno, de massa m , pode deslizar s
No sistema de capacitores em série visto na Figura 17.12, o bloco do centro pode ser deslocado na vertical. Mostre que a capacitância equivalente C do sistema independe da posição daquele bloco e calc
Na Figura 17.16, as faces grandes tanto das placas do capacitor quanto do bloco metálico que se insere entre as placas são quadradas, com lado L . Certos vínculos permitem que o bloco metálico deslize
Qual é a capacitância de uma gota formada pela fusão de duas gotas esféricas de mercúrio com 2,00 mm de raio?
Um capacitor de 2,0 μF e um capacitor de 4,0 μF são ligados em paralelo a uma fonte com uma diferença de potencial de 300 V. Calcule a energia total armazenada nos capacitares.