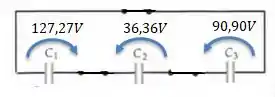
Os capacitores 1,2 e 3 têm capacitâncias iguais a , e , respectivamente. Os capacitores são conectados em paralelo e a combinação é conectada aos terminais de uma fonte de . A seguir, os capacitores são desconectados da fonte de tensão e uns dos outros, e então conectados a três interruptores, como mostra a Figura 24-42.
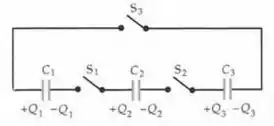
(a) Qual é a diferença de potencial em cada capacitor quando as chaves e estão fechadas, mas permanece aberta?
(b) Depois que a chave é fechada, qual é a carga final na placa esquerda de cada capacitor?
(c) Calcule a diferença de potencial em cada capacitor depois que a chave é fechada.
Passo 1
Antes de conectarmos qualquer chave, reparem que a tensão em cima de cada capacitor é , afinal eles forma todos conectados em paralelo com uma fonte de antes de serem colocados nessas posições...
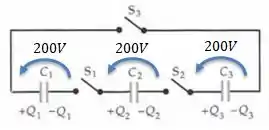
Passo 2
Bem, imagina que as chaves e estão fechadas...
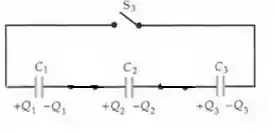
Como o circuito ainda continua aberto, porque não fechou, cada tensão permanece ainda do mesmo jeito que estava...

Passo 3
Quando a chave é fechada...

Vamos ter um rebalanceamento de cargas no circuito, e para vermos como vai ser esse rebalanceamento, tenha sempre em mente que ramo que é negativo, sempre será negativo, ramo que é positivo, sempre será positivo. Mais pra frente você vai entender por que, mas primeiro, vamos calcular qual é as cargas em cada capacitor antes um pouquinho antes da chave se fechar, pode ser?
Sabendo que os capacitores 1,2 e 3 têm capacitâncias iguais a , e e que a relação fundamental de um capacitor é ...
Onde é de inicial (antes da chave se fechar). Antes da chave se fechar a tensão em cima do primeiro capacitor é assim como a tensão em todos os outros, então...
De modo análogo...
Passo 4
SHOW!
Agora vamos olhar novamente para a sentença que citei no passo anterior...
“tenha sempre em mente que ramo que é negativo, sempre será negativo, ramo que é positivo, sempre será positivo”.
Então olha só, nesse ramo que conecta o capacitor ao ...

A soma dessas duas cargas aí é , ou seja, deu um resultado positivo, logo nesse ramo, após o fechamento da chave as cargas vão se rebalancear de modo que as cargas nas duas chapas se tornem positivas, afinal, ramo que é positivo sempre será positivo, sacou?
Então no final, após as cargas se relocomoverem, vai ficar algo assim nesse ramo...
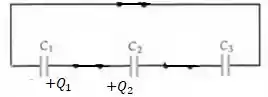
Mas sempre de modo que a soma das duas permaneça ...
Fazendo a mesma análise de antes e depois para os demais ramos, vamos obter...
Ou ainda...
Então, para descobrir as cargas novas no terminal de cada capacitor, basta resolver esse sistema .
Passo 5
Mas infelizmente não podemos trabalhar com as três equações, pois elas são , mas podemos resolver esse problema usando o fato de que num circuito fechado, após um tempo, a soma das tensões tem que ser iguais a ...
Então...
Usando a primeira equação e substituindo a carga ...
Usando a equação e substituindo o ...
Então...
Simplificando as continhas...
Sendo assim, das equações do passo anterior...
Passo 6
Esse resultado aí significa que do lado esquerdo de cada capacitor teremos as seguintes cargas...

Passo 7
BEM... No capacitor , a tensão será...
OBS: O sinal de negativo é indicando que a tensão na realidade está no sentido da direita no capacitor.
No capacitor ...
E no capacitor 3...
Resposta
Letra A: Todas iguais a
Letra B:

Letra C:
