Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 25.4 - Ex. 19

Na Fig. abaixo, as capacitâncias são C 1   =   1,0   μ F e C 2 =   3,0   μ F e os dois capacitares são carregados com diferenças de potencial V   =   100   V de polaridades opostas. Em seguida, as chaves S 1 e S 2   são fechadas. (a) Qual é a nova diferença de potencial entre os pontos a e b? (b) Qual é a nova carga do capacitor 1? (c) Qual é a nova carga do capacitar 2?

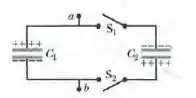
Passo 1

Item (a)

Note que quando as duas chaves são fechadas, os dois capacitores acabam sendo ligados em paralelo. Portanto, a diferença de potencial entre os pontos a e b é V a b = Q C e q em que Q é a carga total dos dois capacitores e C e q é a capacitância equivalente que é igual a C e q = C 1 + C 2 = 4,0 × 10 - 6   F . Agora, devemos calcular as cargas dos dois capacitores, que é:

q 1 = C 1 V = 1,0 × 10 - 6   F 100   V = 1,0 × 10 - 4   C

q 2 = C 2 V = 3,0 × 10 - 6   F 100   V = 3,0 × 10 - 4   C

Como os capacitores são colocados de maneira que as polaridades estão em sentidos opostos, então Q = q 2 - q 1 = 2,0 × 10 - 4   C   ,   então V a b é:

V a b = 2,0 × 10 - 4   C 4,0 × 10 - 6   F = 50   V  

Passo 2

Item (b)

A nova carga do capacitor 1 é:

q 1 = C 1 V = 1,0 × 10 - 6   F 50   V = 5,0 × 10 - 5   C

Passo 3

Item (c)

A nova carga do capacitor 2 é:

q 2 = C 2 V = 3,0 × 10 - 6   F 50   V = 1,5 × 10 - 4   C

Resposta

a   V a b = 50   V  

b   q 1 = 5,0 × 10 - 5   C

c     q 2 = 1,5 × 10 - 4   C

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Na Fig. 25-36, V =10V , C 1=10μ F e C 2=C 3=20μ F . A chave S é acionada para a esquerda e permanece nessa posição até o capacitor 1 atingir o equilíbrio; em seguida, a chave é acionada para a direita
Um capacitor de 2,0 μF e um capacitor de 4,0 μF são ligados em paralelo a uma fonte com uma diferença de potencial de 300 V. Calcule a energia total armazenada nos capacitares.
Na figura, uma diferença de potencial V = 100 V é aplicada a um circuito de capacitores cujas capacitâncias são C 1 = 10,0 μF, C 2 = 5,00 μF e C 3 = 15,00 μF. Determine (a) q 3 ; (b) V 3 ; (c) U 3 ; (
Na figura, uma diferença de potencial V = 100 V é aplicada a um circuito de capacitores cujas capacitâncias são C 1 = 10,0 μF, C 2 = 5,00 μF e C 3 = 4,00 μF. Determine (a) q 3 ; (b) V 3 ; (c) a energi
Na figura, C 1 = 10,0 μF, C 2 = 20,0 μF e C 3 = 25,0 μF. Se nenhum dos capacitores pode suportar uma diferença de potencial de mais de 100 V sem que o dielétrico se rompa, determine(a) a maior diferen