Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 24.1 - Ex. 44

Um capacitor cilíndrico consiste em um longo fio que tem um raio R 1 , comprimento L e carga + Q . O fio está encoberto por uma casca cilíndrica coaxial externa que tem raio interno R 2 , comprimento L e carga - Q .

(a) Determine expressões para o campo elétrico e para a densidade de energia como função da distância R do eixo.

(b) Quanta energia reside na região entre os condutores, que tem raio R , espessura d R e um volume de 2 π R L   d R ?

(c) Integre sua expressão da Parte (b) para determinar a energia total armazenada no capacitor. Compare seu resultado com aquele obtido usando a fórmula U 2 = Q 2 / ( 2 C ) em conjunto com a expressão conhecida para a capacitância de um capacitor cilíndrico.

Passo 1

Cara, pela descrição, podemos ilustrar o nosso capacitor cilíndrico da seguinte forma...

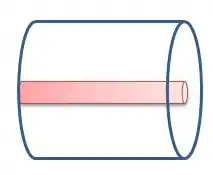
Ou ainda, vendo frontalmente...

Bem, supondo que o fio no cilindro de raio R 1 tem carga + Q ...

A gente vai conseguir medir aí tudo que nos interessa na questão! A começar pelo campo elétrico E , bora?

Passo 2

L e t r a   B :

Cara, de acordo com G a u s s , podemos traçar uma Gaussiana cilíndrica de raio r ...

E Gauss nos diz que o fluxo do campo elétrico ϕ E nessa Gaussiana, como o campo elétrico tem a mesma direção do raio r , pode ser dado por...

ϕ E = E ⋅ A = Q i n t ε 0   →

Onde A é a área da Gaussiana e Q i n t é a carga interna + Q ...

E ⋅ A = + Q ε 0   →

Só que a área da Gaussiana, é a área do cilindro de raio r e comprimento L ...

E 2 π r L = Q + ε 0   →

E = + Q 2 π ε 0 r L

Então essa é a expressão do campo elétrico e sua variação com r , saca?

Passo 3

Para encontrar a expressão da densidade de energia no Campo elétrico, basta lembrar que a densidade de energia varia com...

u e = 1 2 ε 0 E 2   →

Então...

u e = 1 2 ε 0 + Q 2 π ε 0 r L 2   →

u e = 1 2 ε 0 Q 2 4 π 2 ε 0 2 r 2 L 2   →

u e = Q 2 8 π 2 ε 0 r 2 L 2

Passo 4

L e t r a   B :

Imagina agora uma casca cilíndrica no interior que tem um raio R , uma espessura d R ...

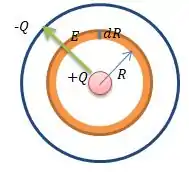
Ora... A energia armazenada no interior desse volume indicado é...

d U = u e ⋅ V o l   →

E o volume dessa casca foi dado no item pra gente como sendo...

d U = Q 2 8 π 2 ε 0 R 2 L 2 ⋅ 2 π R L   d R   →

d U = Q 2 4 π ε 0 R L   d R  

Passo 5

L e t r a   C :

Aqui, basta integrar de R 1 até R 2 a expressão de cima...

∫ d U = ∫ R 1 R 2 Q 2 4 π ε 0 R L   d R   →

U = Q 2 4 π ε 0 L ∫ R 1 R 2 1 R   d R   →

U = Q 2 4 π ε 0 L ln ⁡ R 2 R 1  

E essa é a energia armazenada em todo espaço do cilindro, ta ligado?

Passo 6

Mas o problema nos pediu para confirmar com a expressão...

U = Q 2 2 C →

E sabendo que a capacitância C pela nossa teoria é conhecida para um capacitor cilindrico...

C = 2 π ε L ln ⁡ R 2 R 1

Então...

U = Q 2 2 2 π ε L ln ⁡ R 2 R 1     →

U = Q 2 4 π ε L ln ⁡ R 2 R 1

U = Q 2 4 π ε L ⋅ ln ⁡ R 2 R 1

Que é exatamente a mesma expressão que encontramos no passo anterior, saca?

Resposta

Letra A:

E = + Q 2 π ε 0 r L

u e = Q 2 8 π 2 ε 0 r 2 L 2

Letra B:

d U = Q 2 4 π ε 0 R L   d R

Letra C:

U = Q 2 4 π ε L ⋅ ln ⁡ R 2 R 1

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

10 . Um capacitor cilíndrico consiste em um núcleo condutor maciço, com raio de 0,250c m , cercado por um tubo condutor oco externo. Os dois condutores estão separados por ar, e o comprimento do cilin
9 . Um capacitor é constituído de dois cilindros ocos, coaxiais, de ferro, um dentro do outro. O cilindro interno possui carga negativa e o externo, carga positiva; o módulo da carga sobre cada um é 1
5 . Um capacitor de 10,0μ F com placas paralelas e circulares está ligado a uma bateria de 12,0V . ( a ) Qual é a carga sobre cada placa? ( b ) Quanta carga haveria sobre as placas, caso a distância e
13 . Um capacitor esférico é formado por dois condutores esféricos concêntricos separados pelo vácuo. A superfície esférica interna possui raio de 15,0c m e a capacitância é igual a 116p F . ( a ) Qua
2 . Cada placa de um capacitor com placas paralelas possui área igual a 9,82c m 2 e a distância entre as placas é de 3,28m m . A carga acumulada em cada placa possui módulo igual a 4,35⋅10 - 8C . As p