Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 25.4 - Ex. 21
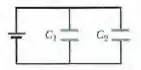
Na Fig. abaixo, dois capacitores de placas paralelas (com ar entre as placas) são ligados a uma bateria. A área das placas do capacitor 1 é e o campo elétrico entre as placas é . A área das placas do capacitor 2 é e o campo elétrico entre as placas é . Qual é a carga total dos dois capacitores?
Passo 1
Olá, meu nobre amigo. Yuri aqui e estarei te ajudando a resolver essa atividade.
Aqui o que temos é a união de 2 capacitores de placas paralelas, e gostaríamos de saber qual a carga total desta ligação.
Aqui temos um problema interessante para resolvermos, vamos calcular a capacitância total do sistema usando:
Porém não temos as cargas e diretamente né, pra encontrar elas precisamos saber encontrar o campo elétrico em um capacitor de placas paralelas, que foi o que a questão nos forneceu.
Passo 2
Pela Lei de Gauss, o campo elétrico gerado por uma placa plana vai ser:
Onde é a área da placa e é a carga da placa. No entanto, o capacitor é composto de duas placas, portanto o campo entre as placas será o dobro (vai ser a soma do campo gerado por uma placa com o campo gerado pela outra).
E como queremos saber a carga, é só coloca-la em evidência:
Passo 3
Para encontrarmos a carga total, só precisamos somar as cargas de cada capacitor:
E como vimos, podemos relacionar a carga com o campo elétrico e a área (
Substituindo os valores , , e temos:
.
Resposta
.