Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 24.Problemas - Ex. 60
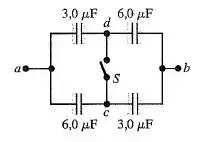
Os capacitores na figura abaixo estão, inicialmente, descarregados e são conectados com indicado no diagrama com a chave aberta. A diferença de potencial aplicada é dada por . (a) Qual é a diferença de potencial ? (b) Qual é a diferença de potencial através de cada capacitor depois de a chave ser fechada? (c) Qual é a quantidade de carga que flui através da chave quando ela está fechada?
Passo 1
letra a)
Quando a chave está aberta, os capacitores estão em série, logo a carga será igual para todos.
Quando a chave é fechada, teremos os pares de capacitores e em paralelo e dois pares em série.
Podemos escrever então que:
Sendo que:
Precisamos agora descobrir essas diferenças de potenciais.
Passo 2
Quando a chave está aberta, temos que cada par de capacitores de e está em série entre si e cada par está em paralelo com o outro par.
Então a capacitância equivalente será:
Passo 3
A carga total será então:
Como os pares de e estão em paralelo e possuem a mesma capacitância, logo os pares terão a mesma carga.
E por esses pares estarem em série entre si, cada capacitor terá a mesma carga:
Passo 4
será então:
Passo 5
letra b)
Quando o interruptor é fechado, cada par de capacitores de e está
paralelos entre si e os dois pares estão em série.
Então por simetria, cada capacitor tem a mesma diferença de potencial de .
Passo 6
letra c)
A única maneira de somar a carga positiva em uma placa de e a carga negativa em uma placa de para mudar é a carga fluir através da chave. Ou seja, a quantidade de carga que flui através da chave é igual à mudança em . Com o interruptor aberto, e . Depois que o interruptor for fechado, , de modo que de carga fluíam através da chave.
Resposta
letra a)
letra b)
letra c)