Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 25.1 - Ex. 100
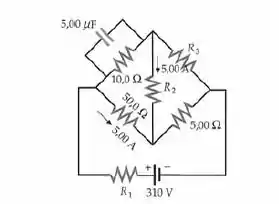
Uma carga constante de está na placa carregada positivamente do capacitor de mostrado na figura abaixo. Determine (a) a corrente na bateria e (b) as resistências .
Passo 1
FALA GALERA, como ta? tudo de boa? Então, vamos para mais uma! Para esse problema aplicaremos a Primeira Lei de Kirchhoff para encontrar o valor da corrente em cada nó do circuito e então utilizar a Segunda Lei de Kirchhoff para obter as equações que encontrarão os valores de , utilizaremos as seguintes equações:
(1)
(2)
Se você não faz a mínima idéia do que diabos seja a Lei de Kirchhoff recomendo dar uma revisada do assunto aqui no Responde aí, procura o tópico e volta pra cá ;D. CONTINUANDO...
Passo 2
Para a alternativa (a), aplicaremos a Primeira Lei de Kirchhoff no nó com o capacitor de e os resistores de e :
Já que a diferença de potencial sobre o capacitor de e o resistor de são os mesmos, temos:
Expressando a diferença de potencial como na equação 2, temos:
Aplicando isso na equação inicial, temos:
E lá se vai à alternativa (a), vamos para a próxima! (Pulinhos de empolgação)
Passo 3
Para a alternativa (b), primeiramente, usaremos a primeira lei de Kirchhoff para encontrar os valores das correntes :
Com isso, podemos aplicar a Segunda Lei de Kirchoff para encontrar o valor dos resistores .
Primeiramente, aplicaremos o loop para a malha que inclui a bateria, o e os resistores de :
Agora, aplicaremos o loop na malha que contém a bateria, o , o e o resistor de :
Por último, aplicaremos o loop na malha que contém o e os resistores de e :
TERMINAMOS, enfim, até a próxima!
Resposta
(a)
(b)