Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 26.Exercício - Ex. 48

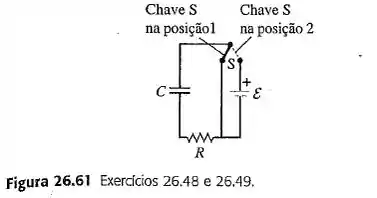
No circuito indicado na Figura 26.61, C = 5,90   μ F , ε = 28,0   V e a fonte da fem possui resistência interna desprezível. Inicialmente, o capacitor está descarregado e a chave S está na posição 1. A seguir, a chave S é colocada na posição 2, de modo que o capacitor começa a se carregar. (a) Após muito tempo depois que a chave é colocada na posição 2, qual é a carga do capacitor? (b) Verifica-se que a carga do capacitor é igual a 110   μ C cerca de 3,0 ms após a chave ser colcocada na posição 2. Qual é o valor da resistência R? (c) Quanto tempo depois que a chave é colocada na posição 2 a carga do capacitor é igual a 99,0 % do valor final da carga encontrado no item (a)?

Passo 1

Quando o capacitor está totalmente carregado, a tensão V no capacitor é igual à bateria fem e

Q   =   C V . Para um capacitor de carregamento,

q = Q ( 1 - e - t / R C )

Uma vez que:

ln ⁡ e x = x

Passo 2

  1. Assim, após muito tempo depois que a chave é colocada na posição 2, a carga do capacitor é:

    2. Q = C V = 5,90 × 10 - 6 F 28,0   V = 1,65 × 10 - 4 C .

    Passo 3

  2. E o valor da resistência R   é dado por:

    3. q = Q ( 1 - e - t / R C )

    Então,

    e - t / R C = 1 - q Q

    E

    R = - t C ln ⁡ ( 1 - q / Q ) .

    E depois, t = 3 × 10 - 3 s :

    R = - 3 × 10 - 3 s ( 5,90 × 10 - 6 F ) ( ln ⁡ ( 1 - 110 / 165 ) ) = 463   Ω

    Passo 4

  3. Se a carga for de 99 % do valor final:

q Q = 1 - e - t R C dá:

t = - R C ln ⁡ 1 - q Q = - 463   Ω 5,90 × 10 - 6 F ln ⁡ 0,01 = 0,0126   s .

A constante de tempo é τ = R C = 2,73   m s . O tempo na parte (b) é um pouco mais do que uma constante de tempo e o tempo na parte (c) é de cerca de 4,6 constantes de tempo.

Resposta

  1. 1,65 × 10 - 4 C
  2. 463   Ω
  3. 0,0126   s
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A chave S da Fig. 27-63 é fechada no instante t = 0 , fazendo om que um capacitor inicialmente descarregado de capacitância C = 15,0 μ F comece a se carregar através de um resistor de resiscência R =
Que múltiplo da constante de tempo τ é o tempo necessário para que um capacitor inicialmente descarregado seja carregado com 99,0% da carga final em um circuito RC série?
Um capacitor com uma carga inicial q 0 é descarregado carregado através de um resistor. Que múltiplo da constante de tempo τ é o tempo necessário para que o capacitor descarregue (a) um terço da carga
Em um circuito RC série, ε = 12,0 V , R = 1,40 M Ω e C = 1,80 μ F . (a) Calcule a constante de tempo. (b) Determine a carga máxima que o capacitor pode receber ao ser carregado. (c) Qual é o tempo nec
A Fig. 27-64 mostra o circuito de uma lâmpada piscante como as que são usadas nas obras de estrada. Uma lâmpada fluorescente L (de capacitância desprezível) é ligada em paralelo com o capacitor C de u