Enunciado
Física - Moysés - Vol. 3- Ed: 1º - Capítulo 2.Problemas - Ex. 7
Uma carga é distribuída uniformemente sobre um fio semicircular de raio . Calcule a força com que atua sobre uma carga de sinal oposto colocada no centro.
Passo 1
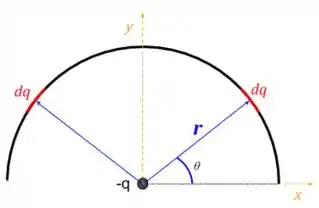
Vamos começar considerando a informação de que a carga está distribuída uniformemente sobre todo o arco. Sendo assim, se pegarmos um pedacinho inifinitesimal dessa barra teremos uma carga em um pedaço . Tipo nessa figura abaixo.
Passo 2
A densidade linear de carga é
onde o comprimento infinitesimal é
Portanto
Passo 3
Sabendo que a força provocada pelo pedaço infinitesimal pode ser escrita como
Passo 4
Da figura podemos decompor o vetor nas coordenasdas e . Obtendo que
Usando a simetria em relação ao eixo podemos perceber que a força resultante do lado direito na direção irá se anular com sua correspondente do lado esquerdo. Sendo assim teremos força apenas na direção .
Passo 5
Podemos reescrever a força infinitesimal subistituindo e anulando o termo das forças na direção
Passo 6
Para achar a força que todo o fio faz é necessário integrar a força provocada pela carga infinitesimal para todo o arco.
Levando em consideração que varia de a . Temos
Agora só precisamos resolver a integral
Lembrando o valor encontrado e lembrando que
Temos