Enunciado
Física - Moysés - Vol. 3- Ed: 1º - Capítulo 2.Problemas - Ex. 8
Um fio muito longo (trate-o como infinito) está eletrizado com uma densidade linear de carga . Calcule a força com que atua sobre uma carga puntiforme colocada à distância do fio.
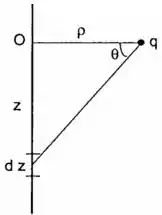
Sugestão: Tome a origem em (fig.) e o fio como eixo . Exprima a contribuição de um elemento do fio à distância da origem em função do ângulo da figura. Use argumentos de simetria.
Passo 1
Vamos resolver essa parada!A sugestão dele é que devemos considerar o ponto como a origem. Ele também disse que o fio é infinito.
Para melhorar a nossa compreensão, podemos imaginar um fio com comprimento , sendo o ponto médio do fio, como na figura a seguir.
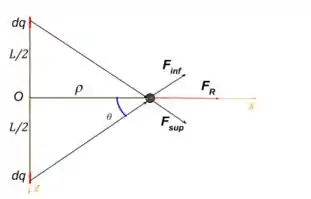
Repara que separamos dois elementos nos fio, onde cada elemento exerce uma força sofre a carga q. Considerando a simetria em relação ao eixo , podemos notar que as forças na direção irão se anular. Sendo assim, a resultante será uma força que aponta na direção .
Passo 2
Podemos escrever a força que um elemento infinitesimal faz sobre q é
onde
Usando teorema de Pitágoras temos que
Considerando que a densidade linear é
podemos reescrever a expressão, usando a simetria, para a resultante em
Passo 3
Sabendo que
podemos reescrever novamente a expressão para a força
Passo 4
Para saber a força que todo o fio exerce sobre a carga , precisamos integrar a expressão da força de uma parte infinitesimal para contemplar todo o fio. Portanto, temos que
Sabendo que apenas quem varia é , podemos escrever
Agora só precisamos resolver essa integral.
Passo 5
Para resolvê-la, vamos usar uma substituição
Portanto
Agora só precisamos lembrar da relação trigonométrica
Assim conseguimos escrever que
Lembra que usamos . Como ele manda consideramos o fio infinito diremos que
Substituindo os limites de integração no resultado da integral teremos como resultado final
Retornando a expressão da força temos