Uma carga positiva está distribuída uniformemente ao longo de todo o comprimento do eixo e uma carga negativa está distribuída uniformemente ao longo de todo o eixo . A carga por unidade de comprimento nos dois eixos é idêntica, exceto pelo sinal. Determine a direção e o sentido do campo elétrico em ponto nas linhas definidas por e . Explique sua resposta.

Inicialmente, vamos lembrar que o campo elétrico devido a um fio infinito sempre aponta na direção radial ao fio. Veja no exemplo abaixo:

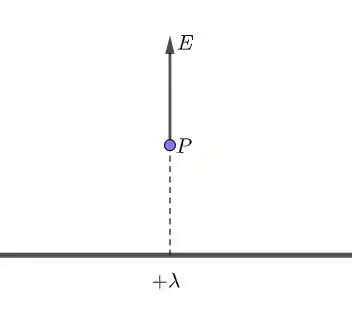
Na figura acima está representado um fio infinito de densidade linear de cargas . O fio faz um campo elétrico no ponto . Lembre-se que . Assim, pontos que estão a uma mesma distância do fio sentem um mesmo campo elétrico.

Vamos agora atacar o nosso problema. Veja a figura

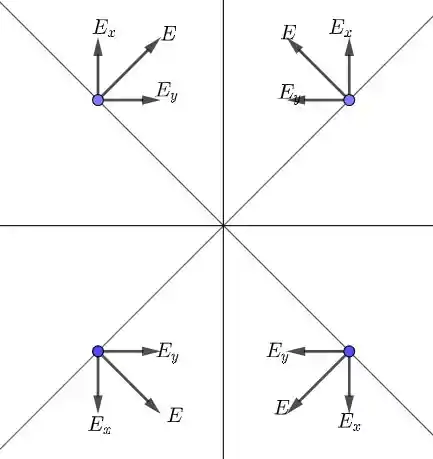
Na figura é o campo elétrico criado pelo eixo ; é o campo elétrico criado pelo eixo . Notemos que todos os pontos das retas e estão a uma mesma distância do eixo e . Sendo assim, . Dessa forma, a resultante deve ser perpendicular às retas e !