Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Moysés - Vol. 3- Ed: 1º - Capítulo 3.Problemas - Ex. 14

Uma camada infinita carregada compreendida entre os planos y = - a e y = a (fig.) tem densidade columétrica de carga ρ constante. Não há cargas fora dela.

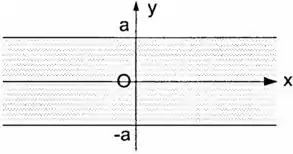
  1. Calcule o campo elétrico E → dentro, acima e abaixo da camada;
  2. Verifique se E →   satisfaz a equação de Poisson.

Passo 1

Se liga! Para verificar o campo dentro da camada podemos utilizar uma superfície gaussiana para simetria esférica. Veja a figura.

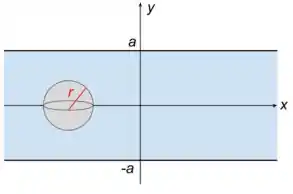
Agora precisamos lembrar da nossa famosa lei de Gauus

ϕ s = ∮ E d A = E A = q i n t ϵ 0

Lembra que a densidade é a carga sobre o volume?

ρ = q i n t 4 3 π r 3 ⇒ q i n t = 4 3 π ρ r 3

E qual é a área de interesse? Sim a área correspondente a superfície da nossa esfera de raio r

A = 4 π r 2

Passo 2

Então, agora só precisamos retornar para nossa expressão e substituir os q i n t e A

E = ρ r 3 ϵ 0

Levando em consideração que o campo aponta para fora da esfera na direção radial, temos

E → = ρ r 3 ϵ 0   r ^

Passo 3

Para saber o campo fora, teremos que adotar um outro tipo de simetria, agora usaremos um cilindro. Se liga como vai ficar

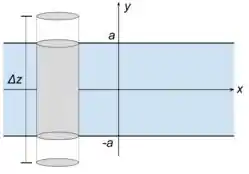
Podemos novamente usar a lei de Gauss

ϕ s = ∮ E d A = E A = q i n t ϵ 0

Agora a área de interesse é a superfície lateral do cilindro

A = 2 π r   Δ y

E a carga vai ser a carga dentro cilindro

q i n t = ρ π r 2 2 a

Assim o campo fora fica

E → =   ρ a ϵ 0 Δ z r ^

Passo 4

Pela equação de Poisson, temos

d i v   E → = ρ ϵ 0

Vamos verificar para o campo dentro

d i v   E → = lim Δ V → 0 ⁡ 1 Δ V ∮ E d A = l i m Δ V → 0 ρ r 4 π r 2 3 ϵ o 4 3 π r 3 = ρ ϵ 0

Vimos que para a parte de dentro é satisfaz!

Passo 5

Para a parte de fora faremos do mesmo jeito, basta trocar o campo! Beleza?!

d i v   E → = lim Δ V → 0 ⁡ 1 Δ V ∮ E d A = l i m Δ V → 0 ρ a r 2 π r Δ z ϵ o Δ z π r 2 2 a = ρ ϵ 0

Ou seja, também satisfaz!

Resposta

a )         E → = ρ r 3 ϵ 0   r ^     d e n t r o ;   E → =   ρ a ϵ 0 Δ z r ^     ( f o r a )

b )       S a t i s f a z

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Na Fig. abaixo, uma barra não condutora "semi-infinita" (ou seja, infinita apenas em um sentido) possui uma densidade linear de cargas uniforme λ . Mostre que o campo elétrico E → p no ponto P faz um
Dois planos paralelos estão uniformemente carregados, com densidades de cara σ e - σ , respectivamente. Calcule o campo elétrico em pontos acima de ambos, abaixo de ambos, e entre os dois. Represente
Uma carga puntiforme q é colocada numa caixa cúbica de aresta l . Calcule o fluxo do campo elétrico sobre cada uma das faces se a carga ocupa o centro do cubo.
Se E é a magnitude do campo num ponto P situado a uma distância D de um plano uniformemente carregado com densidade superficial de carga σ . A maior contribuição para E provém dos pontos mais próximos
Uma barra fina de vidro e encurvada na forma de um semicírculo de raio r. Uma carga +Q está distribuída uniformemente ao longo da metade superior, e uma carga −Q, distribuída uniformemente ao longo da