Uma carga puntiforme de está localizada em , , e uma carga puntiforme de está localizada em , . (a) Determine o módulo, a direção e o sentido do campo elétrico em , . (b) Determine o módulo, a direção e o sentido da força em um próton colocado em , .
Passo 1
Falaaaaii galerinha, show de bola??
Bora pra mais uma??
Só vamooooo!!
A expressão para o campo elétrico em um ponto p devido ao grupo de cargas puntiformes é a seguinte
Onde, k é a constante, é a carga de teste e r é o vetor posição
Passo 2
Vamos utilizar os dados fornecidas, e desenhar um diagrama, onde será usado para encontrar a magnitude e direção do campo elétrico.
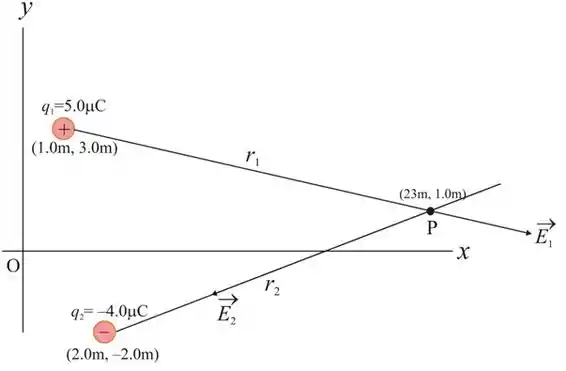
- Vamos expressão vetor posição de carga em relação ao ponto P
- Vamos expressão vetor posição de carga em relação ao ponto P
Da mesma forma, o vetor posição da carga em relação ao ponto P
Passo 3
A expressão para o campo elétrico atuando no ponto P devido à carga é a seguinte:
Vamos substituir os valores numéricos
Passo 4
O campo elétrico que atua no ponto P devido à carga é
Vamos substituir os valores numéricos
Passo 5
Portanto, o campo elétrico resultante no ponto P devido às duas cargas é
Vamos substituir os valores numéricos
Passo 6
A magnitude do campo elétrico resultante no ponto P é expressa como:
Substituindo os valores numéricos
Portanto, a magnitude necessária do campo elétrico resultante é de .
A direção do campo elétrico no ponto P é expressa da seguinte forma:
Substituindo os valores numéricos
A direção do campo elétrico no ponto P é .
Passo 7
Vamos utilizar os dados fornecidas, e desenhar um diagrama, onde será usado para encontrar a magnitude e direção do campo elétrico.
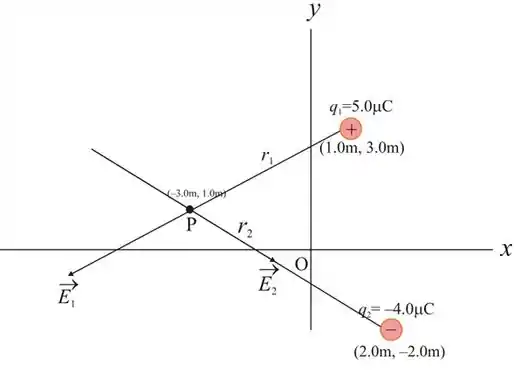
Passo 8
Da mesma forma, o vetor posição da carga em relação ao ponto P
Passo 3
A expressão para o campo elétrico atuando no ponto P devido à carga é a seguinte:
Vamos substituir os valores numéricos
Passo 4
O campo elétrico que atua no ponto P devido à carga é
Vamos substituir os valores numéricos
Passo 5
Portanto, o campo elétrico resultante no ponto P devido às duas cargas é
Vamos substituir os valores numéricos
Passo 6
A magnitude do campo elétrico resultante no ponto P é expressa como:
Substituindo os valores numéricos
Portanto, a magnitude necessária do campo elétrico resultante é de .
A direção do campo elétrico no ponto P é expressa da seguinte forma:
Substituindo os valores numéricos
Passo 7
Portanto, a quantidade de força que atua sobre o próton é
Portanto, a magnitude necessária é de
E a direção do movimento do próton está em um ângulo de .
Resposta
-
Portanto, a magnitude necessária do campo elétrico resultante é de .
A direção do campo elétrico no ponto P é .
Portanto, a magnitude necessária é de
E a direção do movimento do próton está em um ângulo de .