Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 21.Exercício - Ex. 13
Três cargas puntiformes estão dispostas em linha reta. A carga está na origem. A carga está em . A carga está em . Determine (módulo e sinal), quando a força resultante sobre for igual a zero.
Passo 1
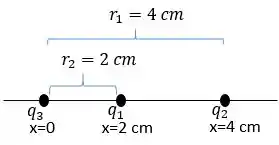
Antes de iniciarmos a resolução desta questão vamos separar os dados importate ditos no enunciado.
Passo 2
Um método eficiente de encontrarmos o valor de é igualando a força com a força .
Retirando os termos semelhantes,temos.
Passo 3
Isolndo
Resposta
Exercícios de Livros Relacionados
Uma carga puntiforme de 5,0μ C está localizada em x = 1,0m , y = 3,0m , e uma carga puntiforme de - 4,0μ C está localizada em x = 2,0m , y = - 2,0 . (a) Determine o módulo, a direção e o sentido do ca
Duas cargas positivas iguais, q , estão no eixo y , uma carga puntiforme está em y = + a e a outra está em y = - a . (a) Mostre que, no eixo x , a componente x do campo elétrico é dada por E x = 2 k q
A estrutura molécula N H 3 é aproximadamente a de um tetraedro equilátero, onde três íons H + formam a base e um íon N - 3 está no ápice do tetraedro. O comprimento de cada lado é 1,64 × 10 - 10m . Ca
Duas cargas puntiformes, cada um com + 4,0μ C , estão no eixo x ; uma das cargas está na origem e a outra em x = 8,0m . Determine o campo elétrico no eixo x em (a) x = - 2,0m , (b) x = 2,0m , (c) x =
Uma carga puntiforme de - 5,0μ C está localizada em x = 4,0m , y = - 2,0m , e uma carga puntiforme de 12,0μ C , está localizada em x = 1,0m , y = 2,0m . (a) Determine o módulo, a direção e o sentido d