Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 5.2 - Ex. 18
Tr��s trenós estão sendo puxados horizontalmente sobre uma superfície de gelo horizontal e sem atrito, através de cordas horizontais (Figura ). A força de puxar é horizontal e possui módulo de . Ache
a) a aceleração do sistema e
b) a tensão nas cordas e .
Passo 1
Fala galera, tudo bem? Vamos resolver essa questão!
O enunciado nos deu três trenós que estão sendo puxados horizontalmente sobre uma superfície sem atrito através de cordas. E nós precisamos encontrar (a) a aceleração do sistema e (b) e a tensão nas cordas e .
Para encontrar a aceleração do sistema, vamos considerar que os três trenós são como um único bloco de massa , que é a soma das massas de todos eles. E assim, usando a segunda lei de Newton na forma:
Depois, para calcular a tensão nas cordas, vamos isolar os blocos e usar segunda lei de Newton em cada um dos trenós considerados.
Vamos lá!
Passo 2
Para resolver essa questão nós vamos usar a convenção de forças e aceleração positiva para a direita. Assim, (a) para determinar a aceleração devemos olhar o sistema como um todo, como se fosse um bloco só de massa.
Para isso vamos somar a massa de todos os trenós:
E nesse único bloco há uma força pra direita de puxando. O desenho fica assim:
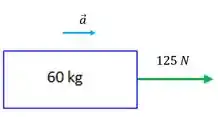
A única força ao longo da direção do movimento é a força de “puxar”, representada em verde e ela vale . Usando a segunda lei temos:
E isolando :
Temos a nossa aceleração:
Passo 3
b) Agora para determinar as tensões nos fios e devemos isolar os blocos e aplicar a segunda lei nele. Vamos calcular uma de cada vez!
Vamos começar pela tensão do fio , o barco de .
Para a direita temos a força de “puxar” de (em verde). Para a esquerda temos a força de tensão no fio que vamos chamar de (em azul). A aceleração a que ele está submetido é igual à aceleração do sistema e vale .
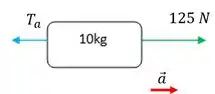
Aplicando a segunda lei temos:
Isolando a tensão na corda , obtemos:
Beleza?
Passo 4
Agora olhando para o barco de temos que apenas a força de tensão no fio (em roxo) é importante para o movimento. A aceleração é a mesma, já que o sistema se move todo em conjunto.
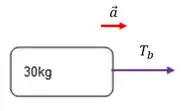
Então agora vamos aplicar para esse barco a segunda lei:
E obtemos a tensão na corda :
Valeu, galera! Até a próxima! 😉