Enunciado
Física - Moysés - Vol. 3- Ed: 1º - Capítulo 2.Problemas - Ex. 6
Cargas q, 2q e 3q são colocadas nos vértices de um triângulo equilátero de lado a. Uma carga Q de mesmo sinal que as outras três é colocada no centro do triângulo. Obtenha a força resultante sobre Q (em módulo, direção e sentido).
Passo 1
Temos que achar a força resultante! Então, primeiro vamos colocar todas as forças que estão atuando sobre na carga Q. Como as cargas possuem o mesmo sinal os vetores da força eletrostática apontam para fora:
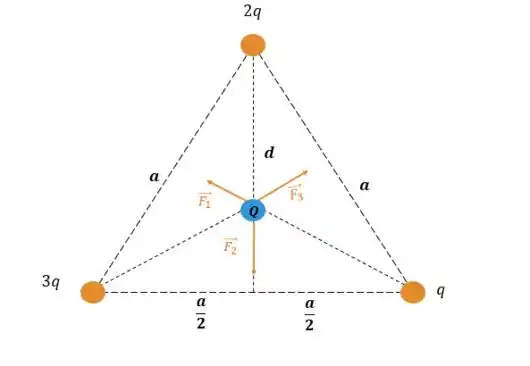
Como é um triângulo equilátero, temos que a carga Q está a uma distância de todas as outras cargas. Vamos colocar essa distância em função do lado .
Passo 2
Pelas propriedades do triangulo equilátero, temos que a sua altura é igual a . E como a carga está bem no seu centro a sua distância da metade de um dos lados é de .
Pelo teorema de Pitágoras da distância
Passo 3
Como queremos achar a força resultante:
Vamos escrever as componentes das forças na direção e :
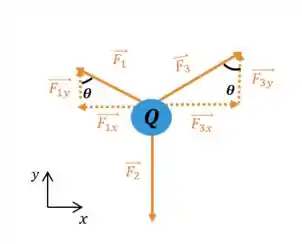
Onde por ser um triângulo equilátero.
Passo 4
Calculando a força resultante na direção :
Onde , então , :
Ou seja, a força resultante da direção vertical é nula. Vamos ver se a força resultante tem componente horizontal
Passo 5
Calculando as componentes na direção :
Substituindo os valores:
Como , assim
Com isso, a força resultante só possui componente na direção
Resposta
O módulo da força resultante é , sua direção é na horizontal e para direita.