Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 9.1 - Ex. 21
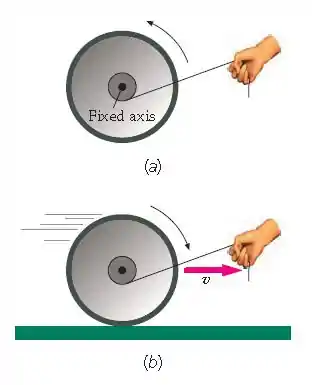
Um carretel é livre para girar em torno de um eixo fixo, e umm cordão enrolado em torno do eixo do carretel faz com que ele gire no sentido anti-horário (Figura 9-42a). No entanto, se o carretel é colocado sobre uma mesa horizontal, o carretel (se houver força de atrito suficiente entre ele e a mesa) gira no sentido horário e rola para a direita (Figura 9-42b). Considerando o torque em relação a eixos apropriados, mostre que estas conclusões são, ambas, consistentes com a segunda lei de Newton para a rotação.
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Ele descreve duas situações e quer que a gente mostre que as duas situações estão de acordo com a segunda lei de Newton para a rotação. E qual é essa segunda lei de Newton?
É essa aqui:
Ela quer dizer que o torque resultante sobre um objeto tem o mesmo sentido da aceleração angular desse objeto.
Então vamos olhar essas duas situações e refletir. Bora lá!
Passo 2
Na situação 1, o carretel está livre, aí uma força aplicada no eixo do carretel (cilindro cinza) causa um torque no setido anti-horário, fazendo ele girar nesse sentido:
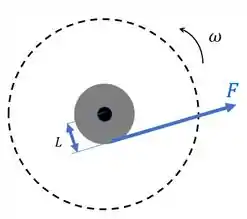
E isso está de acordo com a segunda lei de Newton porque temos apenas um torque, o causado por . Esse torque é dado pelo produto entre a força e a distância do ponto de aplicação da força e o centro. Só que essa distância deve ser perpendicular a força.
Então, no nosso caso, ele vale:
E esse torque gera uma aceleração angular no sentido anti-horário, que gera uma rapidez angular nesse sentido, fazendo o carrete girar nesse sentido.
Ou seja, temos aceleração angular no sentido do torque.
Passo 3
Agora olha a segunda situação:
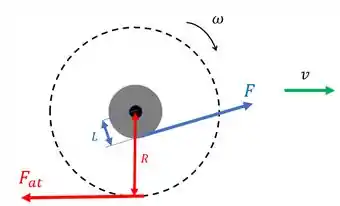
Nessa situação, ainda temos a mesma força causando o mesmo torque da situação anterior. Por que o sentido do carretel inverte? Porque agora a mesa entre em cena, e o contato entre a mesa e a parte mais externa do carretel gera a força de atrito.
A imagem do enunciado diz que o carretel se mexe para a direita. A força de atrito quer se opor ao movimento, então ele fica para a esquerda. Essa força então gera um torque no sentido horário no valor de
Repara que é maior que , então se for grande suficiente, ela pode gerar um torque maior do que o torque gerado por . Considerando que estamos nessa situação, onde , o torque resultante vai ser
Eles tem sinais inversos porque tem sentidos inversos. Se , esse torque resultante está no sentido de que é horário.
Então a aceleração angular gerada está nesse sentido também. Por isso que o carretel passa a girar no sentido horário. E assim, essa situação está de acordo com a segunda lei de Newton para a rotação.
Resposta
Discussão nos passos