Exercícios de Rolamento com Deslizamento - Lista de Exercícios Resolvida

Uma aro de massa e raio é lançado horizontalmente com uma velocidade inicial sobre uma superfície horizontal cujos coeficientes de atrito cinético e estático são e .

Calcule qual é a distância desde o ponto em que o aro toca a superfície até quando ele passa a rolar sem deslizar.

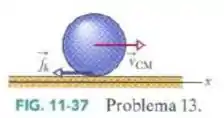
Um jogador de boliche arremessa uma bola de raio ao longo de uma pista. A bola (Fig. 11-37) desliza sobre a pista com velocidade inicial e a velocidade angular inicial . O coeficiente de atrito cinético entre a bola e a pista é . A força de atrito cinético , que age sobre a bola produz uma aceleração linear e uma aceleração angular. Quando a velocidade diminui o suficiente e a velocidade angular aumenta o suficiente, a bola pára de deslizar e passa a rolar suavemente. (a) Qual é o valor de em termos de nesse instante? Durante o deslizamento, quais são (b) a aceleração linear e (c) a aceleração angular da bola? (d) Por quanto tempo a bola desliza? (e) Que distância a bola desliza? (f) Qual é a velocidade linear da bola quando começa a rolar suavemente?

Uma aro de massa e raio é lançado horizontalmente com uma velocidade inicial sobre uma superfície horizontal cujos coeficientes de atrito cinético e estático são e .

Calcule qual é a distância desde o ponto em que o aro toca a superfície até quando ele passa a rolar sem deslizar.

Quando o aro começa a rolar sem deslizar, sua velocidade angular é . Qual é a velocidade linear do centro de massa do aro , do ponto mais alto do aro e do ponto onde o aro toca o solo em relação a um referencial parado no solo?

Suponha agora que a partir do ponto onde o aro começa a rolar sem deslizar, com velocidade do centro de massa igual a , ele começa a subir, rolando sem deslizar, uma rampa que faz um ângulo em relação a horizontal. Qual é a altura máxima atingida pelo centro de massa do aro? Utilize para aceleração da gravidade.

Uma pedra esférica, uniforme e maciça parte do repouso e rola pra baixo de uma colina de de altura. A metade superior da colina é áspera o suficiente para fazer a pedra rolar sem deslizar, mas a metade inferior está coberta de gelo e não há atrito. Dado: momento de inércia de uma esfera girando ao redor do eixo que passa pelo seu centro de massa:

1. Desenhe as forças que agem sobre a pedra quando ela desce a parte superior da colina, justificando o sentido da força de atrito.
2. Qual é o modulo da velocidade de translação da pedra quando ela atinge a base da colina?
3. Qual é o módulo da velocidade angular da pedra na base da colina?

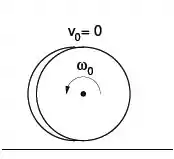
Um disco sólido uniforme é posto em rotação com velocidade angular em torno de um eixo horizontal, perpendicular ao plano do disco, passando por seu centro de massa. Depois, a borda do disco é posta em contato com uma superfície horizontal, e o disco é solto, com

seu eixo de rotação paralelo à superfície, como na figura ao lado. Seja o raio do disco, sua massa e seu momento de inércia em torno do centro de massa, e seja o coeficiente de atrito cinético entre o disco e a superfície. Em termos de ,, e da aceleração da gravidade :

a)Qual é o tempo necessário para que o disco deixe de derrapar?

b)Qual é a velocidade angular do disco no momento em que ele deixa de derrapar?

c)Qual é a distância percorrida enquanto o disco está derrapando?

d) Calcule a razão entre a energia cinética final e a energia cinética inicial do disco.

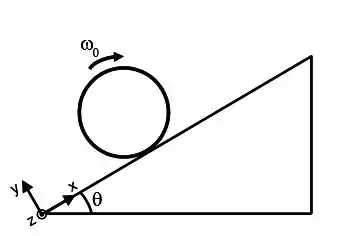
Após sofrer um impulso, um aro de massa e raio rola sem deslizar plano acima. O plano está inclinado de em relação à horizontal. No instante de tempo o aro tem velocidade angular de módulo e está na posição a partir da origem. Suponha que o plano é suficientemente longo e que o aro alcança sua altura máxima a uma distância . Após parar momentaneamente o aro rola sem deslizar plano abaixo. Utilize para a aceleração da gravidade e o sistema de eixos indicado.

(a) Determine o momento de inércia rotacional do aro em relação ao ponto de contato com o plano inclinado.

(b) Determine a distância em função dos dados do problema.

(c) Determine o torque da força de atrito em torno do centro do aro, quando ele estiver momentaneamente parado, prestes a rolar sem deslizar plano abaixo.

(Cap 9 – Ex 101) Uma bola de boliche, de massa e raio , é lançada de forma que, ao atingir o piso, está se movendo horizontalmente com um rapidez , sem girar. Ela desliza uma distância durante um tempo antes de começar a rolar sem deslizar. (a) Se é o coeficiente de atrito cinético entre a bola e o piso, determine , e a rapidez final da bola. (b) Determine a razão entre a energia cinética final e a energia cinética inicial da bola. (c) Determine , e para e .

Uma esfera de raio experimenta rolamento sem deslizamento num plano inclinado que forma um ângulo com a horizontal. Durante um percurso de descida, se o momento de inércia é a aceleração será:

(A)

(B)

(C)

(D)

(E)

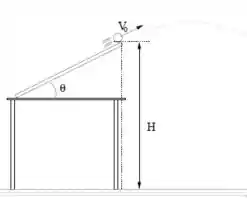
Na figura ao lado vê-se uma montagem. A bolinha de massa é lançada para cima por uma rampa que faz um ângulo com a horizontal, saindo da rampa a uma altura a partir do solo. Mede-se que a bolinha leva um tempo para atingir o solo, a partir do instante que sai da rampa.

P1.2 – calcule a distância horizontal que a bolinha percorrerá do instante que ela saiu da rampa até o momento que se choca com o solo.

Considere uma roda de massa , raio e momento de inércia girando com velocidade angular inicial , sentido horário, baixada sobre uma superfície plana horizontal rugosa com seu centro de massa em repouso inicialmente. O coeficiente de atrito cinético entre a roda e o plano é . A seguir a roda se move no sentido positivo do eixo , deslizando e girando durante um intervalo de tempo . Após o instante de tempo , segue rolando sem deslizar.

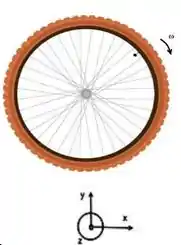
Indique no desenho, as forças que agem sobre a roda durante . Determine na forma literal uma expressão para o coeficiente de atrito cinético em função dos dados citados.

Seja um cilindro maciço e homogêneo, de raio e massa ,(cilindro 1) que pode girar sem atrito em torno de um eixo vertical que passa pelo seu centro. O eixo está fixado em uma mesa horizontal, sobre a qual se encontra o cilindro. Enrolada na superfície curva do cilindro há uma corda inextensível, que passa por uma roldana e tem na extremidade livre um outro cilindro (cilindro 2) de massa que cai sob a ação da gravidade. As massas da roldana e da corda são desprezíveis e a corda não desliza.

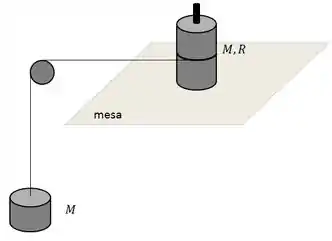
Seja agora a situação em que não há um eixo no interior do cilindro que esteja fixo à mesa, de

modo que o cilindro 1 está livre para deslizar, sem atrito, sobre a mesa. Permanecem as

condições anteriores sobre a corda, a roldana e o cilindro que cai. Nesta nova situação,

b) Escreva as equações de movimento do cilindro 1 e do cilindro 2 (isto é, escreva as equações que relacionam as forças existentes com as acelerações) .

c) Obtenha a relação entre a aceleração do cilindro 2 e as acelerações do cilindro 1.

d) Calcule a tensão na corda.