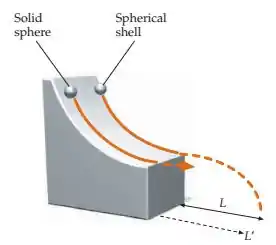
Largadas do repouso da mesma altura, uma casca esférica fina e uma esfera maciça, de mesma massa e mesmo raio , descem rolando um plano inclinado, sem deslizar, da mesma altura vertical (figura 9-64). As duas são lançadas horizontalmente ao abandonarem a rampa. A casca esférica atinge o solo a uma distância horizontal da base da rampa e a esfera maciça atinge o solo a uma distância horizontal da base da rampa. Determine a razão .

As distâncias alcançadas são proporcionais às velocidades que tinham quando saem da rampa, porque o tempo de queda é o mesmo.

Conservando a energia do momento em que as esferas saem da rampa até quando estão prestes a tocar o chão (a potencial gravitacional vira cinética):

Todos os momentos de inércia são da forma , e sabemos também que . Daí:

Substituindo essa expressão na equação da razão dos comprimentos: