Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 11.4 - Ex. 13
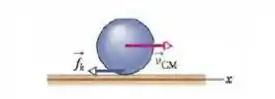
Um jogador de boliche arremessa uma bola de raio ao longo de uma pista. A bola (figura abaixo) desliza na pista com velocidade inicial e velocidade angular inicial . O coeficiente de atrito cinético entre a bola e a pista é . A força de atrito cinético que age sobre a bola produz uma aceleração linear e uma aceleração angular. Quando a velocidade diminui o suficiente, a bola para de deslizar e passa a rolar suavemente.
Qual é o valor de em termos de nesse instante?
Durante o deslizamento, qual é
a aceleração linear
a aceleração angular da bola?
Por quanto tempo a bola desliza?
Que distância a bola desliza?
Qual é a velocidade linear da bola quando começa a rolar suavemente?
Passo 1
Fala aii galerinha bonita, tudo tranks!? Cola aqui comigo pra gente praticar um pouco!
Aqui temos dois momentos:
- deslizamento que faz com que a bola perca velocidade linear (aumentando assim a rotação).
- o rolamento sem deslizamento que já estamos acostumados.
No momento em que o corpo passa do momento com deslizamento para sem deslizamento, ele adquire velocidade angular devido a sua rotação, como a esfera desliza no sentido positivo do eixo enquanto gira no sentido negativo horário, podemos relacionar a velocidade angular com a velocidade do centro de massa através da equação:
Como , temos que:
Passo 2
Belezera, então primeiro vamos olhar para a parte com deslizamento. O que acontece aqui é que existe uma força de atrito que não permite que a bola de boliche deslize. Saca só, na vertical temos a força normal apontando para cima e a peso para baixo.
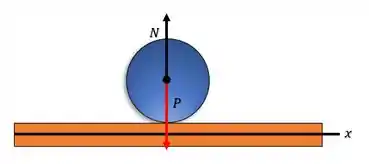
Ambas com mesmo módulo, pois a bola não está em deslocamento vertical. Tal que:
Agora se a gente olhar pro movimento na horizontal, temos apenas a força de atrito atuando sobre a bola de boliche:
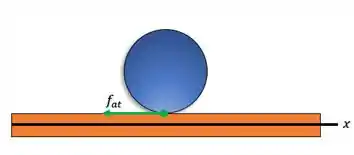
A equação para a força de atrito que conhecemos é dada como:
O sinal negativo indica o sentido contrário ao do movimento. E além disso, o enunciado nos diz que essa força de atrito fornece uma aceleração linear para a bola de boliche, tal que:
Logo:
Isolando :
Portanto:
Passo 3
Então belezinha, agora vamos determinar a aceleração angular.
Sabemos que o torque é dado pela equação:
Onde é o momento de inércia do objeto enquanto que é a aceleração angular. MAASSS, também sabemos que o torque pode ser dado por essa outra equação aqui:
Onde é a força que atua sobre o objeto a uma distância do eixo de rotação, gerando. Igualando as duas equações, obtemos que:
No nosso caso, temos que a força que gera esse torque, é a força de atrito , a uma distância , enquanto que o momento de inércia da bola de boliche é igual ao de uma esfera maciça, , logo:
Isolando , vamos obter que:
Logo:
Passo 4
Agora para determinar o tempo que a bola desliza, vamos usar a relação lá do passo :
Agora sabemos as acelerações, então podemos relacionar essas velocidades com o tempo com que elas variam:
A velocidade angular inicial é zero, a velocidade inicial é dada e vale , e as acelerações acabamos de encontrar nos passos anteriores. Então é só substituir:
Isolando :
Logo:
Passo 5
O deslocamento pode ser dado pela equação horária do movimento. Das equações da cinemática temos:
Substituindo os valores que descobrimos, vamos ter que:
Passo 6
E por fim, também da cinemática, a velocidade final vai ser um pouco menor do que a inicial, pois ela sofre com a força de atrito:
Show!
Bora treinar mais?