Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 9.Exercícios e Problemas - Ex. 31
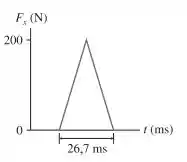
Um carrinho de 500 g é liberado a partir do repouso, 1,0 m acima da base de uma rampa sem atrito e inclinada de 30°. O carrinho rola rampa abaixo e ricocheteia em um bloco de borracha localizada na base. A Figura P9.31 mostra a força exercida durante a colisão. Depois que o carrinho ricocheteia, qual distância ele percorre subindo a rampa?
Passo 1
Temos o seguinte esquema:
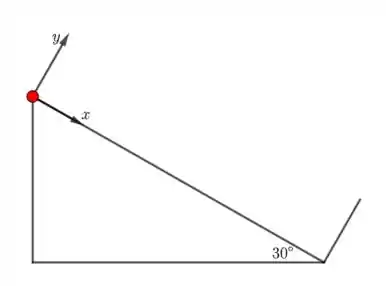
Inicialmente, vamos calcular qual é a aceleração do carrinho ao longo da rampa. Para isso, vamos aplicar a 2° Lei de Newton:
Agora, para calcularmos a velocidade com que o corpo chega na base do plano inclinado, podemos aplicar Torricelli:
Ora, sabemos que e . Assim, temos
Passo 2
Agora que conhecemos a velocidade do carrinho um momento antes de colidir com o plano, poderemos calcular a velocidade do carrinho logo após colidir com o bloco.
Como fazemos isso? Sabemos que a força que o plano faz sobre o carrinho deve estar orientado ao logo do eixo , mas subindo o plano, conforme mostra a figura abaixo:
Sendo assim, o impulso da força será negativo. Podemos escrever:
Como sabemos, o impulso é igual a variação da quantidade de movimento:
Passo 3
Agora, sabemos que a bolinha sobe o plano com velocidade inicial de e com aceleração igual a (no sentido positivo do eixo x, logo é um movimento retardado). Aplicando Torricelli, temos:
Resposta
Sobe 0,50 m.