Um carrinho de brinquedo elétrico é colocado sobre um estreito trilho circular de 60 cm de diâmetro, cuja ranhura força-o a se mover em um círculo. O trilho, de 1,0 kg, é livre para girar em torno de um eixo vertical sem atrito. As hastes radiais do trilho possuem massas desprezíveis. Após o carrinho ser ligado, ele logo atinge uma rapidez final constante de 0,75 m/s em relação ao trilho. Qual é, então, a velocidade angular do trilho, em rpm?
Passo 1
O carro de brinquedo é uma partícula localizada na borda da pista. A pista é um aro cilíndrico girando em torno de seu centro, que é um eixo de simetria. Nenhum torque líquido está presente na pista; portanto, o momento angular do carro e da pista é conservado.
Vamos visualizar a situação:
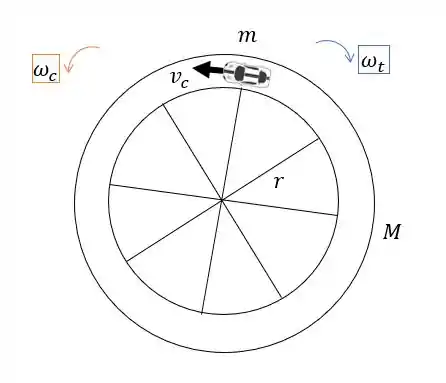
Nós conhecemos , e queremos encontrar então .
Passo 2
A velocidade constante de do carro de brinquedo em relação à pista significa que:
onde t v é a velocidade de um ponto na pista no mesmo raio do carro. Conservação do momento angular implica que:
Os estados inicial e final se referem a antes e depois que o carro de brinquedo foi ligado. A tabela 12.2 foi usada para a pista.
Passo 3
Desde que , nós temos que:
O sinal de menos indica que a pista está se movendo na direção oposta do carro. A velocidade angular da pista é
Convertendo para rpm, fazemos:
A velocidade da pista é menor que a do carro, porque é mais massiva.