Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 4.Exercícios e Problemas - Ex. 85
85. De cima de um trem, um canhão cujo cano forma um ângulo " com a horizontal dispara um projétil para a direita com rapidez em relação ao trem. O disparo é feito exatamente no momento em que o trem, deslocando-se para a direita com rapidez em trilhos retos e horizontais, começa a acelerar com aceleração a. Encontre uma expressão para o ângulo do qual o projétil deve ser disparado a fim de aterrissar o mais distante possível do canhão. Ignore a pequena altura do canhão acima dos trilhos.
Passo 1
Tudo bem senhores!? Aqui vamos nós de novo pra mais uma questãozinha de Cinemática!
E pra resolver esse tipo de questão, já sabe né?
Como é de costume; primeiramente bora fazer um esboço pra ajudar a entender melhor o nosso problema...
De modo que obtemos então, a seguinte imagem abaixo...
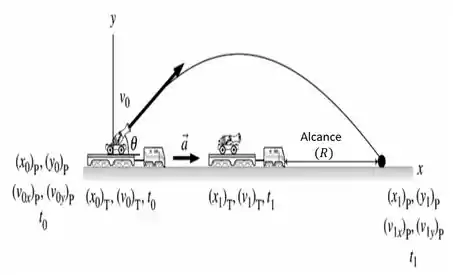
Sendo que a imagem acima retrata o que a gente quer que aconteça, né!? Afinal; já pensou se o projetil for disparado e cair no trem ferindo algum passageiro. Isso não, meu amigo!
E pelo que sabemos dos problemas de lançamento horizontal e movimento oblíquo e também do que lemos no enunciado, tiramos que...
Onde o objetivo aqui é encontrar o ângulo do qual o projétil deve ser disparado a fim de aterrissar o mais distante possível do canhão.
Ous seja, o ângulo que maximiza a expressão abaixo do Alcance...
Por isso, mãos à obra!
Passo 2
Bora pro que interessa! Chega de introdução!
Tomando como o instante inicial do lançamento... Pra facilitar a nossa resolução, bora dividir o movimento do projétil depois que sai do canhão, em duas partes; vertical e horizontal...
Na horizontal, em , o projétil não tem aceleração influenciando seu movimento. Sendo assim, ele executa um movimento uniforme, com velocidade constante.
Olhando pra nossa figura do , ficamos então com...
Isso aí é para o projétil. Para o trem, a equação fica assim... Lembrando que ele tá acelerado, hein!?
Voltando à equação do projétil, temos que tomar cuidado aí. Nosso projétil é lançado de um canhão de um trem em movimento. Desse modo, a velocidade total do projétil em , vai ser a soma da velocidade do trem com a velocidade de lançamento do projétil na horizontal, ...
E chegamos então, a seguinte fórmula abaixo... Com as variáveis que temos;
Obtemos a equação que descreve a trajetória do nosso amigo segundo a direção ...
Passo 3
Indo agora pra direção vertical, temos nessa direção a presença da aceleração da gravidade para baixo influenciando a trajetória do cara da moto.
Desse modo, peguemos a equação abaixo da velocidade para o movimento uniformemente variado... É claro, usando as variáveis da nossa figura, né!?
Calma que eu já vou explicar o significado dessas variáveis, ainda não identificadas!
Bem! A equação anterior refere-se ao momento em que o projétil é lançado até alcançar sua altura máxima. Logo, temos que...
E consequentemos obtemos o tempo desprendido até a altura máxima;
Como o tempo total de descida do projétil é o mesmo do de subida, então o tempo total do movimento é dado por...
Passo 4
Obtido o tempo total, temos que a distância horizontal percorrida pelo projétil é dada por...
E a distância percorrida pelo trem é de...
Sendo assim, ficamos com...
Passo 5
Pra finalizar e obter o ângulo que maximiza , afinal o que queremos é que trem e projétil fiquem o mais distante possível um do outro; basta derivar em relação a e igualar a .
Como é nada mais nada menos do que uma constante, então bora ignoral ela...
Ficamos então, com a seguinte equação para resolver...
Agora se liga só! Cês já tão carecas de saber que o ângulo de tem uma tangente igual a...
No caso da nossoa fórmula, para que a tangente fosse precisaria acontecer o seguinte;
Sendo assim, podemos estabeler algumas condições importantes... São elas:
E só pra ressaltar. Caso o trem não acelerasse, teríamos que...
E consequentemente;
Logo, tá mais que provado que o ângulo perfeito pro nosso lançamento é de .
Pronto! Finalizamos aqui!
Até a próxima!