Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 10.10 - Ex. 66

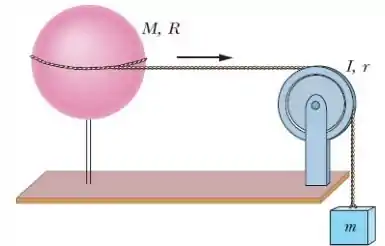
Uma casca esférica homogênea de massa M = 4,5 kg e raio R = 8,5 cm pode girar em torno de um eixo vertical sem atrito (Fig. 10-44). Uma corda de massa desprezível está enrolada no equador da casca, passa por uma polia de momento de inércia I = 3,0 X 10-3 kg · m2 e raio r = 5,0 cm e está presa a um pequeno objeto de massa m = 0,60 kg. Não há atrito no eixo da polia e a corda não escorrega na casca nem na polia. Qual é a velocidade do objeto depois de cair 82 cm após ter sido liberado a partir do repouso? Use considerações de energia.

Passo 1

Shooow galerinhaaa !! Bora seguir?

O problema nos disse para levar em considerações a energia, certo?

Como nós não temos atrito, a energia é conservada ! O que vai acontecer é que a energia potencial gravitacional inicial será convertida eme energia cinética. Já a energia cinética tem três termos: a rotação da casca esférica, a rotação da polia e a translação do bloco, beleza? :D

m g h = I ω c a s c a 2 2 + I ω p o l i a 2 2 + m v 2 2

Sabendo que a velocidade angular é dada por:

ω c a s c a = v R

ω p o l i a = v r

E que o momento de inercia da casca é dada por:

I = 2 3 M R 2

Nós vamos substituir:

m g h = 1 2 2 3 M R 2 v R 2 + I 2 v r 2 + m v 2 2

m g h = 1 3 M R 2 v 2 R 2 + I 2 v 2 r 2 + m v 2 2

m g h = 1 3 M v 2 + I 2 v 2 r 2 + m v 2 2

m g h = 1 3 M + I 2 r 2 + m 2 v 2

Isolando a velocidade, que é o que queremos:

v = m g h m 2 + I 2 r 2 + M 3 = 2 g h 1 + I m r 2 + 2 M 3 m

Passo 2

Já achamos o principal, que é a fórmula que vamos usar !! Então a única coisa que precisamos agora é olhar os valores:

g = 9,8 m s 2

h = 82   c m = 0,82   m

M   =   4,5   k g

R   =   8,5   c m = 0,085

I   =   3,0 ×   10 - 3   k g   m 2

r   =   5,0   c m = 0,05   m

m   =   0,60   k g

Substituindo os valores, temos:

v = 2 ( 9,8 ) ( 0,82 ) 1 + 3.10 - 3 ( 0,60 ) ( 0,050 ) 2 + 2 ( 4,5 ) 3 ( 0,6 ) = 1,4 m s

Beeeem legal , não foi ?!

Resposta

v = 1,4 m s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

As partículas da figura estão ligadas por uma barra muito leve. Elas giram em torno do eixo y a 2,0r a d / s . (a) Determine a rapidez de cada partícula e utilize esses valores para calcular a energia
Calcule a energia cinética da Terra, associada à rotação em torno de seu eixo, e compare sua resposta com a energia cinética do movimento orbital do centro de massa da Terra em torno do Sol. Suponha a
Uma esfera maciça, de 1,4 k g e 15 c m de diâmetro, está girando em torno de seu diâmetro a 70r e v / m i n . (a) Qual é sua energia cinética? (b) Adicionando-se 5,0 m J de energia à energia cinética,
Um disco uniforme, de massa M e raio R , pode girar livremente em torno de um eixo fixo horizontal que passa pelo seu centro de massa perpendicularmente ao seu plano. Uma pequena partícula de massa m
Um anel uniforme de 1,5 m de diâmetro pivota em torno de um ponto de seu perímetro, livre para girar em torno de um eixo horizontal perpendicular ao seu plano. O anel é largado com seu centro à mesma