Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 1- Ed: 14º - Capítulo 2.Problemas - Ex. 86

Um carrinho de controle remoto parte do repouso e segue em movimento retilíneo. Um smartphone montado no carrinho tem um aplicativo que transmite o módulo da aceleração do carro (medido por um acelerômetro) a cada segundo. Os resultados são dados nesta tabela:

Cada valor medido tem algum erro experimental. (a) Desenhe um gráfico de aceleração versus tempo e determine a equação para a linha reta que oferece o melhor ajuste dos dados. (b) Use a equação para a(t) que você encontrou na parte (a) para calcular v(t), a velocidade do carro em função do tempo. Desenhe o gráfico de v × t. Esse gráfico é uma linha reta? (c) Use seu resultado da parte (b) para calcular a velocidade do carro em t 5,00 s. (d) Calcule a distância que o carro trafega entre t 0 e t 5,00 s.

Passo 1

A velocidade x instantânea de uma partícula em movimento em linha reta é igual para a taxa instantânea de mudança na coordenada x da partícula.

v x = d x d t

A velocidade x instantânea de uma partícula em movimento em linha reta é igual para a taxa instantânea de mudança na velocidade da partícula.

a x = d v x d t

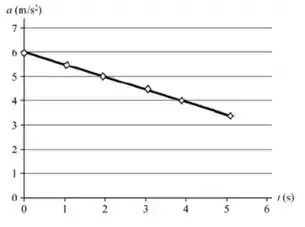
A magnitude da aceleração do carro é medida a cada segundo eos resultados são apresentados na tabela do livro.

Passo 2

Letra a:

Fazendo um ajuste linear (podemos usar qualquer programa para isso):

a t = - 0.5131 m s 3 t + 6.0262 m s 2                                   ( 1 )

Passo 3

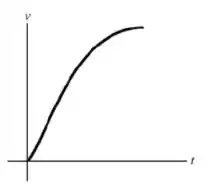
Letra b:

A velocidade do carro é encontrada integrando a Equação (1) em relação a tempo:

v ( t ) = ∫ a ( t ) d t = ∫ - 0.5131 m s 3 t + 6.0262 m s 2 d t = - 0.5131 t 2 2 + 6.0262 t + C = - 0.25655 t 2 + 6.0262 t + C

onde C é uma constante arbitrária encontrada usando as condições iniciais.

Seja a velocidade em t = 0 zero:

v 0 = - 0.25655 0 + 6.0262 0 + C = 0 C = 0

Portanto, a expressão para a velocidade do carro é:

v t = - 0.25655 t 2 + 6.0262 t                                             ( 2 )

Passo 4

Letra c:

Substitua t = 5 s na Equação (2):

v ( 5 ) = - 0.25655 ( 5 ) 2 + 6.0262 5 = 23.7 m s

Passo 5

Letra d:

A distância percorrida pelo carro entre t = 0   e   t = 5 s é encontrada integrando a Equação (2) com respeito ao tempo:

d = ∫ 0 5   v ( t ) d t = ∫ 0 5   - 0.25655 t 2 + 6.0262 t d t = - 0.25655 t 3 3 + 6.0262 t 2 2 0 5 = - 0.08551 t 3 + 3.0131 t 2 0 5 = - 0.08551 ( 5 ) 3 + 3.0131 ( 5 ) 2 = 64.6 m

Resposta

  1. a t = - 0.5131 m s 3 t + 6.0262 m s 2
  2. v t = - 0.25655 t 2 + 6.0262 t
  3. 23.7 m s
  4. 64.6 m
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

2.9 Um carro para em um semáforo. A seguir ele percorre um trecho retilíneo de modo que sua distância ao sinal é dada por x t = b t 2 - c t ³ ³, onde b=2,40m / s ² ² e c=0,120m / s ³ ³ . a) Calcule a
2.15 Uma tartaruga se arrasta em linha reta, à qual chamaremos de eixo O x com a direção positiva para a direita. A equação para a posição da tartaruga em função do tempo é x ( t )=50,0c m+( 2,0c m /
2.14 A Figura 2.34 mostra a velocidade em função do tempo de um carro movido a energia solar. O motorista acelera a partir de um sinal de parada e se desloca durante 20 s com velocidade constante de 6
2.12 Em um teste de um novo modelo de automóvel da empresa Motores Incríveis, o velocímetro é calibrado para ler m/s em vez de km/h. A série de medidas a seguir foi registrada durante o teste ao longo
2.13 O carro mais rápido (e mais caro)! A tabela mostra dados de teste para o Bugatti Veyron, o carro mais veloz já fabricado. O carro se move em linha reta (eixo 0x).a) Desenhe um gráfico v x t da ve