Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 5.4 - Ex. 53
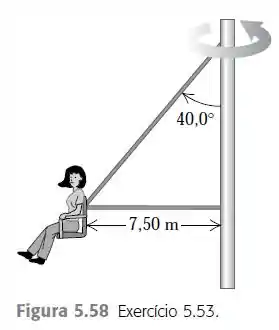
Em outra versão do ‘balanço gigante’ (Exercício 5.52),o assento é conectado a dois cabos, como indicado na Figura 5.58, uma das quais é horizontal. O assento balança em um círculo horizontal, a uma taxa de 32,0 rpm (rev/min). Considerando que o assento pesa 255 N e uma
pessoa de 825 N está sentada sobre ele, ache a tensão em cada cabo.
Passo 1
Eaee, belezinha?? Bom... o enunciado nos dá o seguinte balanço gigante de um parque de diversões com suas dimensões:
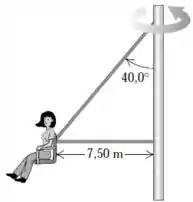
Queremos encontrar a tensão em cada um dos cabos que sustenta o passageiro.
Para isso, o enunciado nos dá as seguintes informações:
- O assento balança em um círculo horizontal, a uma taxa de ;
- o assento pesa e a pessoa de está sentada sobre ele.
Para resolvermos isso, temos que fazer um diagrama de corpo livre do sistema e analisar as forças que estão atuando no corpo.
Também, utilizaremos também a segunda Lei de Newton:
Onde é a força resultante, é massa e é a aceleração.
Passo 2
Bom... O objeto é composto da pessoa mais o assento.
Este objeto se move em uma horizontal circular e tem aceleração centrípeta, , direcionada para o centro do círculo.
O raio se dá por:
Vamos adotar como à direita na direção da aceleração centrípeta. E para cima.
A massa total é dada por:
Substituindo os valores e sabendo que é a soma dos pesos da pessoa e do assento:
Passo 3
Então, vamos esboçar o diagrama de corpo livre dessa situação:
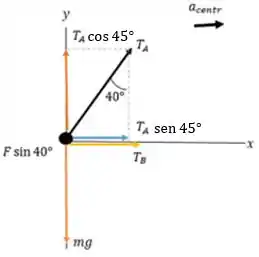
Como a taxa de rotação é , o período, é dado por:
Passo 4
Vamos aplicar a 2º Lei de Newton para a balança:
Para o :
Passo 5
No :
Resposta
A tensão no cabo horizontal () é de 8370 N e a tensão no outro cabo () é de 1410 N.