Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 5.4 - Ex. 56

Uma roda-gigante no Japão possui um diâmetro de 100 m . Ela faz uma revolução a cada 60 segundos. a) Calcule a velocidade de um passageiro quando a roda-gigante gira a essa taxa.

b) Um passageiro pesa 882 N em uma balança no solo. Qual é seu peso aparente no ponto mais alto e no ponto mais baixo da roda-gigante? c) Qual deveria ser o tempo de uma revolução para que o peso aparente no ponto mais alto fosse igual a zero? d) Nesse caso, qual deveria ser o peso aparente no ponto mais baixo?

Passo 1

Eaee, belezinha?? Bom... o enunciado nos diz que uma roda-gigante no Japão possui um diâmetro de 100 m . Ela faz uma revolução a cada 60   segundos.

Queremos calcular a velocidade de um passageiro quando a roda-gigante gira a essa taxa.

Também temos outras perguntinhas relacionadas ao peso de um passageiro de 882 N (considerando uma balança no solo).

Para resolvermos isso, temos que fazer um diagrama de corpo livre do sistema e analisar as forças que estão atuando no corpo.

Também, utilizaremos também a segunda Lei de Newton:

F r = m a

Onde F r é a força resultante, m é massa e a é a aceleração.

Obs: lembre-se que a força peso P é dada pelo produto da massa m pela aceleração da gravidade g :

P = m g

Passo 2

Bom... O peso aparente de uma pessoa é a força normal exercida sobre ele pelo assento que está sentado, ou seja, aplicando a segunda lei de Newton sobre ele, temos que a massa é:

∑ F = m a

⇒ m = P g = 882 N 9,8 m / s 2 = 90 k g

Sabemos que a aceleração é centrípeta, então ela é:

a c e n t r = v 2 R

Onde v é a velocidade e R é o raio.

Temos que o diâmetro é d = 100 m , então o raio se dá por:

R = d 2 = 100 m 2 = 50 m

Também temos que o período, T , é igual a 60 s .

Mas também sabemos que:

T = 2 π R v

Passo 3

  1. Bom, agora nós vamos expressar v em termos do período, T , para encontrar e a velocidade do passageito na roda gigante:

    2. v = 2 π R T

    v = 2 π ⋅ 50 m 60 s = 5,24 m / s

    Note que sua aceleração é:

    a c e n t r = ( 5,24 m / s ) 2   50 m = 0,5549 m / s 2

    Passo 4

  2. Vamos esboçar o diagrama de corpo livre para a pessoa no topo de seu caminho:

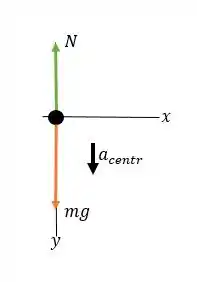
    3. Observe que a aceleração é para baixo, então vamos tomar como + y para baixo.

    Temos forças atuando somente no e i x o   y , então plicando a segunda lei de Newton sobre o corpo, temos que:

    ∑ F y = m a y

    m g - N = m a c e n t r

    ⇒ N = m ( g - a c e n t r )

    Portanto,

    N = 90 k g ⋅ ( 9,8 m / s 2 - 0,549 m / s 2 ) = 833 N  

    Passo 5

    Ok!

    Agora, vamos esboçar o diagrama de corpo livre para a pessoa na parte inferior de seu caminho:

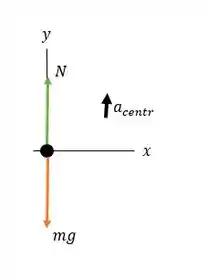
    Aqui, temos que a aceleração é para cima, então vamos toma-la como + y .

    Novamente, temos forças atuando somente no e i x o   y , então plicando a segunda lei de Newton sobre o corpo nesse ponto, temos que:

    ∑ F y = m a y

    N - m g = m a c e n t r

    ⇒ N = m ( g + a c e n t r )

    N = 90 k g ⋅ ( 9,8 m / s 2 + 0,549 m / s 2 ) = 931 N

    Passo 6

  3. Supondo que o peso no ponto mais alto seja seja, isso impica que a sua força normal também seja igual a zero. E então:

m g = m a c e n t r

⇒ m g = m v 2 R

⇒ g = v 2 R

Em termos da velocidade, v , temos que:

v = g R

v = 9,8 m / s 2 ⋅ 50 m

v = 22,1 m / s

Passo 4

O tempo de uma revolução seria, então:

T = 2 π ⋅ 50 m 22,1 m / s = 12,2 s

Passo 5

Então para calcular o peso apararente quando está no ponto inferior, utilizamos a seguinte relação:

N = m g + a c e n t r = 2 m g = 2 ⋅ 882 N = 1760 N

Duas vezes o seu verdadeiro peso.

Resposta

  1. v = 2 π ⋅ 50 m 60 s = 5,24 m / s
  2. No ponto mais alto: N = 90 k g ⋅ ( 9,8 m / s 2 - 0,549 m / s 2 ) = 833 N  

    3. No ponto mais baixo:

    N = 90 k g ⋅ ( 9,8 m / s 2 + 0,549 m / s 2 ) = 931 N

  3. T = 12,2 s
  4. 1760 N
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se lançarmos apropriadamente na parte interna da superfície de um cone, que está na figura abaixo, um bloco é capaz de manter movimento circular uniforme. Desenhe um diagrama de corpo livre para o blo
RICO EM CONTEXTO. Sua companhia de mudanças deve embarcar um caixote de livros em um caminhão com a ajuda de algumas pranchas inclinadas de 30 ° acima da horizontal. A massa do caixote é 100k g e o co
Em 1976, Gerard O'Neill propôs que grandes estações espaciais habitáveis fossem construídas em órbita ao redor da Terra e da Lua. Como quedas livres prolongadas apresentam efeitos médicos adversos, el
Em um parque de diversões, você está sentado em um banco de um compartimento que gira com rapidez constante em um círculo vertical de 5,0 m de raio. O brinquedo é planejado de forma que sua cabeça est
Três forças atuam sobre um corpo em equilíbrio estático (Figura abaixo). (a) Se F 1 ,F 2 e F 3 representam as magnitudes das forças atuantes sobre o corpo, mostre que F 1 s e n θ 23 = F 2 s e n θ 31 =