A peça de uma máquina consiste de uma barra estreita de de comprimento e possui pequenas massas de presas por parafusos nas extremidades. Os parafusos podem suportar uma força máxima de , sem se soltarem. Essa barra gira sobre um eixo perpendicular a ela, no seu centro. a) À medida que a barra gira a uma taxa constante, sobre uma superfície horizontal sem atrito, qual é a velocidade escalar máxima que as massas podem ter, sem que os parafusos se soltem? b) Suponha que a máquina seja redesenhada, de modo que a barra gire a uma taxa constante, perfazendo um círculo vertical. É mais provável que um dos parafusos se solte quando a massa estiver no topo do círculo, ou na base do círculo? Use um diagrama do corpo livre para entender por quê. c) Usando o resultado obtido em (b), qual é a maior velocidade escalar que as massas podem ter, sem que um parafuso se solte?

Temos que a barra se move em um caminho circular, então sua aceleração é dada por:

A aceleração é direcionada para o centro.

Temos um diâmetro de , isso implica em um raio:

Transformando para metros:

a) Vamos adotar o eixo positivo na direção ao centro do círculo. Assim, .

E então, amos aplicar a 2º lei de Newton:

Substituindo a aceleração centrípeta :

E isolando na equação:

Substituindo os valores do enunciado, obtemos a velocidade escalar:

b) Agora, para o : vamos adotar como sendo para baixo quando a massa está no topo do círculo e sendo para cima quando a massa está no fundo do círculo.

Assim, a segunda lei de Newton nos fornece:

Vamos esboçar o diagrama de corpo livre de cada caso antes:

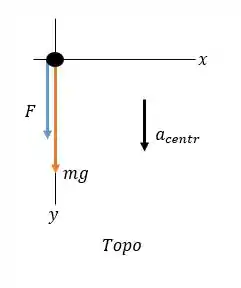
No topo, temos:

E na parte inferior:

Logo, para uma determinada taxa de rotação, o valor da força necessária é maior na parte inferior do caminho.

c) Assim, usando o resultado do passo anteriro, vamos ter:

E então, chegamos a velocidade escalar na forma:

Assim, temos:

Valeu, galera! Até a próxima! 😉