Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 5.4 - Ex. 59
Uma corda é amarrada em um balde de água e o balde gira em um círculo vertical de raio . Qual deve ser a velocidade mínima do balde no ponto mais elevado do círculo
para que a água não seja expelida do balde?
Passo 1
Eaee, belezinha?? Bom... o enunciado nos diz que uma corda é amarrada em um balde de água e o balde gira em um círculo vertical de raio .
Queremos calcular a velocidade mínima do balde no ponto mais elevado do círculo
para que a água não seja expelida do balde.
Bom... Aqui temos um balde de água que se move em um círculo. Opa! Temos uma questão de movimento circular.
Com isso temos que a aceleração centrípeta, , direcionada para o centro do círculo e é dada por:
Onde é a velocidade e é o raio.
A questão nos deu que o raio é: .
Ah... utilizaremos também a segunda Lei de Newton:
Onde é a força resultante, é massa e é a aceleração.
Passo 2
Para gente visualizar melhor, vamos esboçar o que esta acontecendo na situação do enunciado:
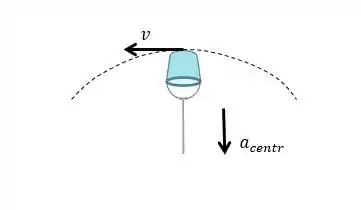
A aceleração centrípeta está em direção ao centro do círculo, nesse ponto, ela é para baixo.
Agora vamos achar a veloc idade mínima para que a água não do balde!
Passo 3
Vamo considerar um diagrama de corpo livre para quando o balde estiver no topo do seu caminho circular, como esboçamos na figura acima:
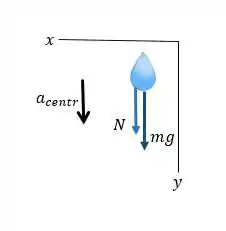
Repare que a força normal, e a força peso, , estão na mesma direção.
Isso significa que é a força normal descendente exercida sobre a água pelo fundo do balde. Uma vez que nosso foco é a água que esta dentro do balde.
Lembrando que a força normal é exercida do balde sobre a água, por isso ela está para baixo no ponto mais alto do círculo.
Passo 4
Então, vamos aplicar a segunda lei de Newton sobre a agua que está dentro do balde no , já que é o único eixo do qual temos forças atuando:
Obs: é a aceleração da gravidade.
Passo 5
Como queremos a velocidade mínima do balde, para que a água não caia. Nessa situação, a água está na iminência de cair.
A velocidade sendo um pouco menor que a velocidade mínima, já é o suficiente para ela cair do balde. Com isso, ela está quaaaase caindo, mas não está!
Diante dessa situação, podemos considerar a força normal sendo nula!! Isso porque a água quaaase não está encostante no balde. Beleza?? Então:
Bom, agora vamos isolar o para que possamos encontrar a velocidade, :
Se é menor que essa velocidade mínima, a gravidade puxa a água (e o balde) fora do caminho circular.