Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 9.6 - Ex. 30
Um carro de brinquedo de pode se mover ao longo de um eixo ; a Fig. 9-50 mostra a componente da força que age sobre o carro, que parte do repouso no instante . A escala do eixo é definida por . Em termos dos vetores unitários, determine (a) em ; (b) em ; (c) em .
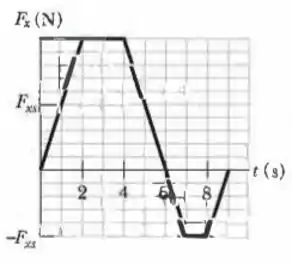
Passo 1
Devemos lembrar que a área de um gráfico de força em função do tempo nos dá o impulso. Assim, para determinar o momento linear em , podemos aplicar o teorema impuslo momento linear, sabendo que o momento linear inicial é nulo (pois o carro parte do repouso) e que para determinar o impulso devemos calcular a área do gráfico de até . Portanto, dividindo o trapézio em um triângulo e um retângulo:
Como a força o momento linear estão no eixo , então:
Passo 2
De maneira análoga para , vamos dividir nossa figura em três triângulos e um retângulo, lembrando que as áreas abaixo do eixo do tempo têm sinal negativo. Assim:
Assim:
Passo 3
Seguindo os mesmos passos para , usando os dois trapézios regulares para calcular as áreas, temos:
Sabendo que:
Isolando :
Então, como também está no mesmo sentido e direção do impulso, então:
Resposta
- ;
- ;
- .