Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 8.Exercícios e Problemas - Ex. 13

13. Um carro trafega sobre o topo de uma colina cujo raio é de . Quanto vale a máxima velocidade que o carro pode ter sem que perca contato com a pista no topo da colina?

Passo 1

Vamos lá pra mais um probleminha sobre dinâmica!

Olha só! O nosso probleminha vai estar perfeitamente representado pela imagem abaixo..

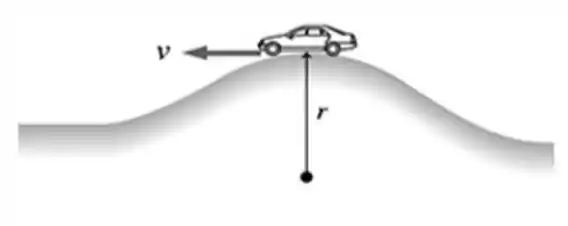
Onde obviamente temos duas forças atuando sobre o carro; que são a força gravitacional e a força de reação normal no topo da colina. Essas duas forças estão representadas no diagrama de corpo livre abaixo, onde adotamos o modelo do carro como partícula pra ficar tudo mais fácil;

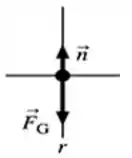
Passo 2

Terminada essa parte introdutória, vamos pro que interessa! Bora usar a Segunda lei de , que diz que a resultante das forças em um sistema é igual ao produto da massa pela aceleração, no caso, a aceleração centrípeta que procuramos...

Onde é a aceleração radial, ou também chamada de centrípeta. Voltando ao que interessa,

Acho que por essa fórmula, já que a força gravitacional só vai depender da massa do carro que a gente não sabe... Tá bem claro, que pra obter a velocidade máxima só há uma coisa a fazer!

Isso mesmo! A normal tem que valer zero, de maneira que a partir disso, o carro começa a perder contato com a pista! Desse modo, iremos maximizar a resultante centrípeta.

Sendo assim;